第一章 质点运动学

约 1399 个字 预计阅读时间 5 分钟

1.1 质点、参考系和坐标系

质点
没有形状与大小，但是具有质量的点

在研究地球相对于太阳的公转时，地球可以被视作一个质点。倘若研究地球的自转，则地球不可以被视作一个质点。

鉴于“静止是相对的，运动是绝对的”的观点，我们会在对物体运动的研究中引入参考系的概念。

参考系
被选作参考的另一物体（通常在该参考系下被视为静止）

在具体的研究中，我们还会引入坐标系来帮助计算，常见的坐标系有：直角坐标系、球坐标系和柱坐标系。

1.2 位移、速度和加速度

1.2.1 位矢

在直角坐标系x-y-z中，如果有一质点A的坐标为(x, y, z)，则其位矢为：

\[ \vec{r} = x·\vec{k} + y·\vec{i} + z·\vec{j} \]

1.2.2 位移与路程

此知识点在初高中已经有了充分的介绍了，故此略过。

特别强调的是前者是有方向的矢量，后者是标量。

注意区分\({\left|\Delta\vec{r}\right|}\)（位移的长度），\({\Delta r}\)（前后位矢长度的差值）

1.2.3 速度

平均速度：\({\displaystyle\vec{v}=\frac{\Delta \vec{r}}{\Delta t}}\)

平均速率：\({\displaystyle v=\frac{\Delta s}{\Delta t}}\)

众所周知，瞬时速度是指当\({\Delta t \rightarrow 0}\)时，其位移关于时间的一阶导数。

因此瞬时速度也有方向，也是矢量。

\[\begin{aligned} \vec{v} &= \lim_{\Delta t \rightarrow 0}\frac{\vec{r}(t_0 + \Delta t)-\vec{r}(t_0)}{\Delta t}\\ &= \frac{{\rm d}\vec{r}}{{\rm d}t} \end{aligned} \]

在直角坐标系中，可以将速度分解为x, y, z三个方向，如下图示意：

1.2.4 加速度

瞬时加速度是瞬时速度关于时间的一阶导数，也是位移关于时间的二阶导数，描述的是速度变化。

加速度也是矢量。

瞬时加速度推导如下：

\[ \vec{a} = \frac{{\rm d}v}{{\rm d}t} = \frac{{\rm d}^2 r}{{\rm d}t^2} \]

注意区分\({\left|\Delta\vec{v}\right|}\)和\({\Delta v}\)。

平均加速度：\({\overline{\vec{a}}=\displaystyle\frac{\Delta\vec{v}}{\Delta t}}\)

接下来我们用微积分的方法反推回高中著名的运动学公式：

例1-1 已知质点作直线匀加速运动，加速度为a，求其位移关于时间的函数。

\[\begin{aligned} &由\vec{a}=\frac{{\rm d}\vec{v}}{{\rm d}t}\Rightarrow {\rm d}\vec{v}=\vec{a}{\rm d}t\\ &以标量形式，有{\rm d}v = a{\rm d}t\\ &对两侧积分，有\int^v_{v_0}{\rm d}v = \int^t_0a{\rm d}t\\ &v=v_0+at\\ &由\frac{{\rm d}x}{{\rm d}t}=v=v_0+at\\ &\int^x_{x_0}{\rm d}x = \int^t_0(v_0+at){\rm d}t\\ &x=x_0+v_0t+\frac{1}{2}at^2\\ &消去时间，有v^2=V^2_0+2a(x-x_0) \end{aligned} \]

1.3 圆周运动极其描述

1.3.1 自然坐标系

为了方便在圆周运动的背景下进行运动学研究，我们通常将矢量方向分解为切向矢量\({\vec{e}_t}\)和法向矢量\({\vec{e}_n}\)，这两个方向与一般坐标系构建不同，称为自然坐标系。

自然坐标系的特点：轨迹上各点自然坐标轴的方位不断变化。

可见下图：

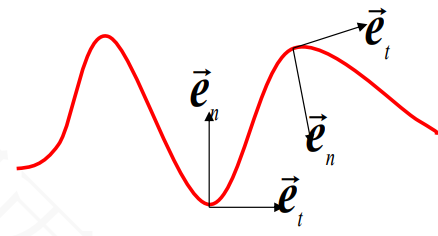
1.3.2 自然坐标系下的加速度

在自然坐标系下：

\[\begin{aligned} &\vec{v}=v_t\vec{e_t}=v\vec{e_t}=\frac{{\rm d}s}{{\rm d}t}\vec{e_t}\\ &a_t = \frac{{\rm d}\vec{v}}{{\rm d}t} = \frac{{\rm d}v}{{\rm d}t}\vec{e_t}+v\frac{{\rm d}\vec{e_t}}{{\rm d}t}\\ &\vec{a}=\frac{{\rm d}v}{{\rm d}t}\vec{e_t}+\frac{v^2}{R}\vec{e_n} \end{aligned} \]

对此，令\({\displaystyle a_t=\frac{{\rm d}v}{{\rm d}t},\quad a_n=\frac{v^2}{R}}\)，\({a_t}\)称切向加速度，\({a_n}\)称法向加速度

1.3.3 圆周运动的角量描述

在一个在平面直角坐标系下，以原点为圆心的圆上运动，若以ox轴为参考，规定逆时针为正方向，则：

\[ 角位移\Delta\theta = \theta - \theta_0\\ 角速度\omega = \lim_{\Delta t \rightarrow 0}\frac{\Delta \theta}{\Delta t}=\frac{{\rm d}\theta}{{\rm d}t}\\ 角加速度\alpha=\frac{{\rm d}\omega}{{\rm d}t}=\frac{{\rm d}^2\omega}{{\rm d}t^2} \]

其中角速度的单位为弧度/秒(\({rad·s^{-1}}\))，角加速度为弧度/平方秒(\({rad·s^{-2}}\))

角加速度\({\alpha}\)对运动的影响：

• \({\alpha=0}\)，质点作匀速圆周运动
• \({\alpha\neq 0且\alpha 为常数}\)，质点作匀变速圆周运动
• \({\alpha}\)随时间变化，质点作一般的圆周运动

1.3.4 质点匀变速圆周运动

转化为一维运动形式，运动学公式与一维运动形式相似。

可举例：\({\displaystyle\Delta\theta=\omega _0t+{1 \over 2}\alpha t^2}\)

1.3.5 线量与角量之间关系

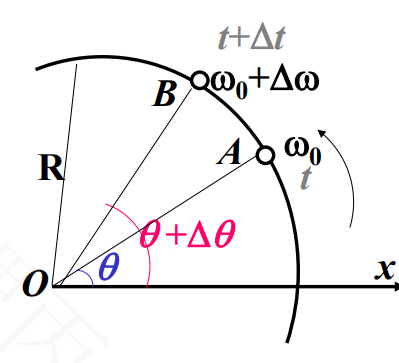
在\({\Delta t}\)时间内有：

\[ \lim_{\Delta t \rightarrow 0}\overrightarrow{AB} = \lim_{\Delta t \rightarrow 0}\overset{\frown}{AB}\\ \]

由上，得出角速度与线速度之间的关系：

\[ v=R\omega \]

1.3.6 切向加速度与角加速度的关系

对于切向加速度，我们有：

\[ a_t =\frac{{\rm d}v}{{\rm d}t}=R\alpha \]

对于法向加速度（向心加速度），我们有：

\[ a_n=\frac{v^2}{R}=R\omega^2 \]

1.4 抛体运动

对于抛体运动，我们通常将运动方向拆解为水平方向与重力方向，如下图所示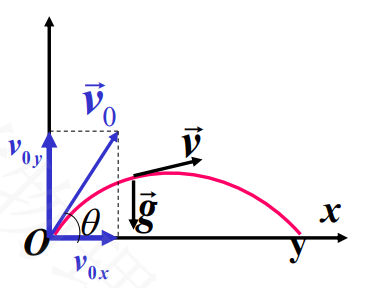

以出射点为参考，在水平方向上速度恒定为\({v_{0x}}\)，竖直方向上的加速度\({\vec{a}_y=\vec{g}=-g\vec{j}}\)，小球在竖直方向上做匀变速运动。

对于小球的整体速度有：

\[ \vec{v}=(v_0\cos\theta)\vec{i}+(v_0\sin\theta-gt)\vec{j} \]

抛体运动在高中已经有所涉及，故此简略带过。