第三章 运动守恒定律

约 1344 个字 预计阅读时间 4 分钟

3.1 功能定律、动能定律

力对空间的积累效应：力的功，即\({\displaystyle\int\vec{F}·{\rm d}\vec{r}=\Delta E}\)

力对时间的积累效应：力的冲量，即\({\displaystyle\int\vec{F}·{\rm d}t=\Delta\vec{p}}\)

3.1.1 功的概念

正如前文，功表示的是力的空间累积效应。

\[ A = \int\vec{F}·{\rm d}\vec{r} \]

功率：

3.1.2 能量

能量
反映各种运动形式共性的物理量。各种运动形式的相互转化用能量来量度，各种运动形式的相互转化遵循能量的转换和守恒定律

与机械运动直接相关的能量是机械能

3.1.3 牛顿第二定律的积分形式

针对变力做功，例如曲线运动，要计算其做功多少，需要采取“微元分割”的思想.

对于其中任意小段路程，可以近似为直线，也就是与位移大小相同，那么有:

\[ {\rm d} A = \vec{F}·{\rm d}\vec{r}\\ 则总功为：\Delta A = \int^b_a\vec{F}·{\rm d}\vec{r} \]

特别地，弹簧的做功过程就是一个很简单的例子，我们将推导高中公式的由来：

\[ A = \int^{x_b}_{x_a}F{\rm d}x = -\int^{x_b}_{x_a}kx{\rm d}x = \frac{1}{2}kx_a^2 - \frac{1}{2}kx_b^2 \]

对于万有引力，假设物体m相对于运动中心M运动，研究过程中万有引力做功：

$$\begin{aligned} {\rm d}A &= \vec{F}{\rm d}\vec{r}\ \therefore A &= \int^{r_b}_{r_a}G_0\frac{mM}{R^2}{\rm d}\vec{r}\

\end{aligned} $$

由以上例子，我们不难做出以下转换：

\[\begin{aligned} A_{ab} &= \int^b_a\vec{F}{\rm d}\vec{r} \\ &= \int^b_ama{\rm d}s \\ &= \int^b_a m\frac{{\rm d}v}{{\rm d}t}{\rm d}s\\ &= \int^b_a mv{\rm d}v\\ &= \frac{1}{2}mv_b^2 - \frac{1}{2}mv_a^2 \end{aligned} \]

这就是质点动能定理。

质点动能定理
合外力对质点所做的功等于质点动能的增量。

对于质点系的动能定理，必须区分出外力和内力，其中内力是质点之间的作用，外力是外界对整个质点系的作用。

质点系动能定理
所有外力和内力对质点系做功之和等于质点系总动能的增量。

3.2 功能定理

3.2.1 质点系的动能定理

\[ A_e + A_i = \Delta E \]

3.1.2 质点系的功能定理

特别地，对于质点系来说，其机械能变化只与外力和非保守内力作用有关。

保守力
如果一个力对物体的做功只与其始末位置有关，而与运动路径无关，则称该力为保守力。

3.3 动量定理与动量守恒定律

3.3.1 质点动量定理

我们知道：

\[ \vec{F} = \frac{{\rm d}\vec{p}}{{\rm d}t} = \frac{{\rm d}(m\vec{v})}{{\rm d}t} \]

所以有：

\[ \int^{t_2}_{t_1}\vec{F}{\rm d}t = m\vec{v}_2 - m\vec{v}_1 \]

我们定义\({\Delta \vec{p} = \vec{I}}\)，\({\vec{I}}\)即为冲量，那么有：

\[ \vec{I} = \int^{t_2}_{t_1}\vec{F}{\rm d}t \]

3.3.2 质点系动量定理

3.3.3 动量守恒定理

特别地，在合外力不为0的情况下，有时候也可以运用动量守恒定律，比如爆炸，碰撞等（内力>>外力）。

例题：

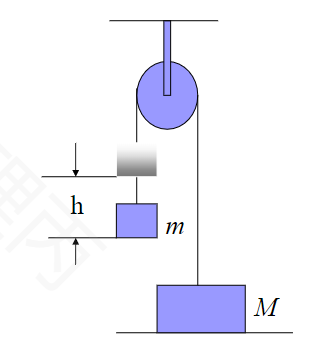
如图，M大于m，当m从高h处自由下落后极短时间内拉紧绳子，求绳子刚被拉紧时两物体的速率？

\[\begin{aligned} &\begin{align} 解：&由动能定理，mgh = \frac{1}{2}mv_m^2 - 0\quad\\ &拉紧时，由动量守恒，(m+M)v - mv_m = 0\quad\\ \end{align}\\ &\qquad那么有v = \frac{m}{m+M}\sqrt{2gh} \end{aligned} \]

3.4 质点的角动量和角动量守恒定律

3.4.1 力矩

首先我们引入力矩的概念：

力距
反映力的转动效应而引入的物理量

在如下坐标系中：

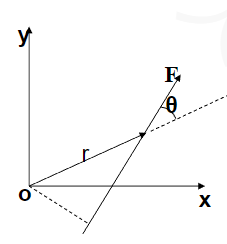
点处有一质量为m的质点，受力F，则力\({\vec{F}}\)关于原点o的力矩\({\vec{M}_0}\)定义为：

\[ \vec{M}_0 = \vec{r}\times \vec{F} \]

值得注意的是这是一个叉乘，叉乘的右手法则是将四指从\({\vec{r}}\)开始向\({\vec{F}}\)弯曲（角度不超过180°），此时大拇指方向即为力矩方向。

力矩的大小：

\[ M_0 = rFsin\theta \]

单位为\({N·m}\)

3.4.2 角动量

角动量
若质点在力作用下，时刻t由矢径\({\vec{r}}\)所确定的位置，其动量为\({m\vec{v}}\)，与力矩类似，有定义： \(\(\vec{L}=\vec{r}\times m\vec{v}\)\)

角动量的单位为\({kg·m/s^2}\)

3.4.3 角动量定理

由角动量定义推导，有：

\[\begin{aligned} \frac{{\rm d}\vec{L}}{{\rm d}t}&=\frac{{\rm d}}{{\rm d}t}\left(\vec{r}\times\vec{p}\right)\\ &=\frac{{\rm d}\vec{r}}{{\rm d}t}\times\vec{p}+\frac{{\rm d}\vec{p}}{{\rm d}t}\times\vec{r}\\ &=\vec{v}\times m\vec{v}+\vec{F}\times\vec{r}\\ &=\vec{M} \end{aligned} \]

因此我们有重要定理：角动量定理

\[ \vec{M}=\frac{{\rm d}\vec{L}}{{\rm d}t} \]

从这个定理，我们可以发现重要结论：

• 力矩决定了角动量的变化快慢
• 角动量的变化速率等于力矩大小

3.4.5 角动量守恒

当\({\vec{M}=0}\)时，有\({\displaystyle\frac{{\rm d}\vec{L}}{{\rm d}t}=0}\)，那么质点的角动量\({\vec{L}=\vec{L}_0=恒矢量}\)，这就是角动量守恒定律。

注意，此处力矩应该考虑合力矩。

日常生活中，天体运动，匀速圆周运动都遵循角动量守恒。