第六章 机械振动

约 1302 个字 预计阅读时间 4 分钟

6.1 简谐振动

简谐振动
物体运动时，离开平衡位置的位移（或者角位移）按余弦/正弦规律随时间变化

6.1.1 简谐振动的运动表达式

假设有一个质点沿固定直线，在其平衡位置附近来回往复运动，则其相对于平衡位置o的位移x有：

\[ x = A\cos(\omega t+ \varphi) \]

由上，推导有：

\[ \begin{aligned} &v = \frac{{\rm d}x}{{\rm d}t}=-\omega A\sin(\omega t + \varphi)\\ &a = \frac{{\rm d}v}{{\rm d}t} = -\omega^2A\cos(\omega t + \varphi) = -\omega^2 x \end{aligned} \]

不难看出，位移、速度和加速度都具有周期性，并且在图像上，位移与速度、速度与加速度各相差90°相位。

6.1.2 简谐运动三参量

• 振幅A：表示质点偏离平衡位置的最大距离
• 周期T：完成一次振动所需时间
• 频率f：1s内的振动次数
• 角频率\({\omega}\)：2π秒内的振动次数
• 相位\({\omega t + \varphi}\)：确定质点在一个周期内的运动状态

为了衡量两个振动的先后关系，可以采用上面的相位概念，假如有下方关系：

\[ \Delta \varphi = (\omega t + \varphi_{20}) - (\omega t + \varphi_{10}) = \varphi_{20} - \varphi_{10} \]

\({\Delta\varphi}\)称为相位差，表示两者在相位上的先后关系。

6.1.3 简谐振动的旋转矢量表示法

研究简谐振动时候，可以采用直观的几何表示——旋转矢量表示法。

旋转矢量法
一长度等于振幅\({\vec{A}}\)的矢量 在纸平面内绕\({O}\)点沿逆时针方向旋转，其角速度与谐振动的角频率相等，这个矢量称为旋转矢量。

其做法是： 1. 以\({O}\)点为原点建立直角坐标系 2. 绘制长度为\({A}\)（振幅）的矢量 3. 设初始时刻\({（t=0）}\)该矢量与\({x}\)轴夹角为\({\varphi}\)（初相位） 4. 假设该矢量以角速度\({\omega}\)做逆时针旋转 5. 该矢量在\({x}\)轴的投影\({x}\)随时间变化即为简谐运动的位移

表示如下：

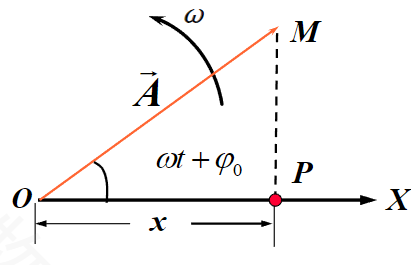
在旋转矢量表示法中对简谐运动之间的超前关系有着更加直观的展示：

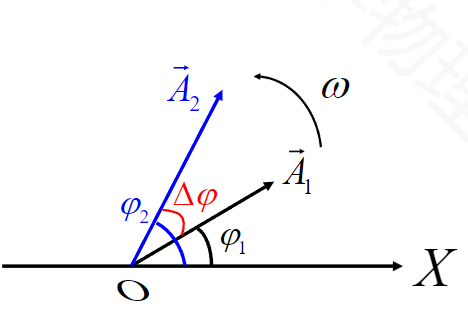
当\({\pi>\Delta\varphi>0}\)时，称第二个振动超前第一个振动\({\Delta\varphi}\)。

6.2 几种常见简谐运动

6.2.1 单摆

以角位移刻画单摆相对平衡位置的位移，转化为对转动的研究：

假设其角位移为\({\theta}\)，则其受力矩为\({mgl\sin\theta}\)，若摆长为\({l}\)，那么有：

\[ \begin{aligned} &\theta\rightarrow 0,\quad\sin\theta\approx 0 \\ &M = mgl\sin\theta \\ \therefore\quad &\frac{{\rm d}^2\theta}{{\rm d}t^2} = \frac{M}{J} = -\frac{mgl\theta}{ml^2} = -\frac{g}{l}\theta \\ &令\omega^2 = \frac{g}{l}，T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{l}{g}}\\ &\theta = \theta_m\cos(\omega t + \varphi_0) \end{aligned} \]

6.3 简谐振动的能量

考虑水平方向的弹簧振子的简谐振动，我们知道\({\omega^2 = \frac{k}{m}}\)

• 动能：\({E_k = \frac{1}{2}mv^2 = \frac{1}{2}m\omega^2A^2\sin^2(\omega t + \varphi)}\)
• 势能：\({E_p = \frac{1}{2}kx^2 = \frac{1}{2}m\omega^2A^2\cos^2(\omega t + \varphi)}\)

所以简谐振动的系统总能量为\({E = E_k + E_p = \frac{1}{2}m\omega^2A^2 = \frac{1}{2}kA^2}\)

由上可以知道，对于以水平弹簧振子为代表的简谐振动是满足机械能守恒的。

6.4 简谐振动的合成

6.4.1 同方向的简谐振动的合成

假设一质点同时参与沿同一方向（x轴）且频率相同的简谐振动，两个简谐振动的运动方程为：

\[ x_1 = A_1\cos(\omega t + \varphi_1)\qquad x_2 = A_2\cos(\omega t + \varphi_2) \]

那么该质点的运动方程是以上两个运动方程之和：

\[ x = x_1 + x_2 = A_1\cos(\omega t + \varphi_1) + A_2\cos(\omega t + \varphi_2) \]

利用旋转矢量图可以表示为：<待补充>

当然，可以知道的是：

• 同相叠加，合振幅最大：\({A = A_1 + A_2}\)
• 反向叠加，合振幅最小\({A = \left|A_1 - A_2\right|}\)

6.4.2 垂直方向的简谐振动的合成

设一个质点同时参与两个同频率的简谐振动，且这两个振动实在互相垂直的x, y轴进行的，其位移表达式为：

\[ x = A_1\cos(\omega t + \varphi_1)\qquad y = A_2\cos(\omega t + \varphi_2) \]

消去参数：

\[ \begin{aligned} &\frac{x}{A_1} = \cos(\omega t + \varphi_1) = \cos\omega t\cos\varphi_1 - \sin\omega t\sin\varphi_1 \\ &\frac{y}{A_2} = \cos(\omega t + \varphi_2) = \cos\omega t\cos\varphi_2 - \sin\omega t\sin\varphi_2 \\ \therefore\quad &\frac{x^2}{A_1^2} + \frac{y^2}{A_2^2} + 2\frac{xy}{A_1A_2}\cos(\varphi_1 - \varphi_2) = \sin^2(\varphi_1 - \varphi_2) \end{aligned} \]

由以上结果，我们作如下分类讨论：

• 分振动相位相同：当\({\varphi_2 - \varphi_1 = 0}\)时，有\({y = \frac{A_2}{A_1}x}\)，轨迹为一直线
• 分振动相位相反：当\({\varphi_2 - \varphi_1 = \pi}\)时，有\({y = -\frac{A_2}{A_1}x}\)，轨迹为一直线
• 分振动相位差为\({\plusmn\frac{\pi}{2}}\)：当\({\varphi_2 - \varphi_1 = \pm\frac{\pi}{2}}\)时，有\({\frac{x^2}{A_1^2} + \frac{y^2}{A_2^2} = 1}\)，轨迹为一椭圆
• 分振动相位差为任意值：轨迹为一椭圆，但椭圆的主轴与坐标轴不重合

特别的，当振幅\({A_1 = A_2}\)，如果相位差为\({\plusmn\frac{\pi}{2}}\)，那么合成出的为轨迹为一个圆。