第七章 参数估计

约 2914 个字 预计阅读时间 10 分钟

7.0 绪论

在具体的统计场景中，我们往往容易判断出分布类型，比如正态分布，但是我们通常不知道其参数，比如\(\mu、\sigma\)是多少。

为此我们需要通过样本来估计总体的分布参数，常用的方法有点估计和区间估计。

7.1 点估计

点估计
点估计，就是根据样本\((X_1,X_2,\cdots,X_n)\)，对每一个总体中的未知参数\(\theta_i(i=1,2,\cdots,k)\)，构造出一个统计量\(\hat{\theta_i} = \hat{\theta_i}(X_1,X_2,\cdots,X_n)\)，作为参数\(\theta\)的估计。

常用的点估计方法有矩法和极大似然法。

7.1.1 矩法

设总体X的分布函数为\(F(x,\theta_1,\theta_2,\cdots,\theta_m)\)，其中\(\theta_1,\theta_2,\cdots,\theta_m\)为未知参数，假定总体X的i阶原点矩\(E(X^i)\)（记\(\mu_i\))存在且存在未知数（否则用下一阶），则：

\[ \begin{cases} \mu_1 = E(X) = g_1(\theta_1,\theta_2,\cdots,\theta_m) \\ \mu_2 = E(X^2) = g_2(\theta_1,\theta_2,\cdots,\theta_m) \\ \vdots \\ \mu_m = E(X^m) = g_m(\theta_1,\theta_2,\cdots,\theta_m) \end{cases} \Rightarrow \begin{cases} \theta_1 = h_1(\mu_1,\mu_2,\cdots,\mu_m) \\ \theta_2 = h_2(\mu_1,\mu_2,\cdots,\mu_m) \\ \vdots \\ \theta_m = h_m(\mu_1,\mu_2,\cdots,\mu_m) \end{cases} \]

依据大数定理，由样本i阶原点矩\(A_i\)估计总体i阶原点矩\(E(X^i)\)，我们知道：

\[ A_i = \frac{1}{n}\sum^n_{j=1}X^i_j \xrightarrow{P} E(X^i) = \mu_i \]

所以参数估计有：

\[ \begin{cases} \theta_1 = h_1(A_1,A_2,\cdots,A_m) \\ \theta_2 = h_2(A_1,A_2,\cdots,A_m) \\ \vdots \\ \theta_m = h_m(A_1,A_2,\cdots,A_m) \end{cases} \]

特别地，在具体的题目中，往往会出现多个样本原点矩符合矩法估计的要求，考虑稳定性与简单性，我们更倾向于采用尽可能低阶的原点矩来估计参数。

当然这也暴露了矩估计的不足之处，其是不唯一的。

利用矩法估计参数一般分为三大步：

1. 写出适当的总体i阶原点矩与参数的关系，联立成为方程组
2. 解出各个参数关于总体i阶原点矩的表达式
3. 依据大数定理回带样本i阶原点矩，算出参数估计值。

特别注意的是，除了第三步，前两步的参数都是准确的，而非估计。

Tip

指数分布\(E(\lambda)\)中，\(\lambda\)矩估计为\(\frac{1}{\overline{X}} = \frac{n}{\displaystyle\sum^n_{i=1}X_i}\)。

正态分布\(N(\mu,\sigma^2)\)中，\(\mu\)的矩估计为\(\overline{X}\)，\(\sigma^2\)的矩估计为\(\displaystyle\frac{1}{n}\sum^n_{i=1}(X_i-\overline{X})^2\)。

7.1.2 最大似然估计

最大似然估计提出背景如下：

假如有一个黑盒子，里面装有数量为1:3的黑球和白球，但是不知道哪种颜色多，有放回地取出五个球，结果为黑黑白黑黑，估计抽到黑球的概率。

基本的估计方法是，假设抽到黑球的概率p=0.25或者0.75，然后求在特定概率下出现抽取结果的概率，比较概率高低，选取最有可能发生的那一个。

在这一题，p=0.75时候最容易出现这个结果，所以判断黑球多。

一般，若总体为离散型，设\(X\sim P(X=x)=p(x;\theta),\ \theta\in\Theta\)，其中\(\theta\)未知，从总体X中抽取样本\(X_1,X_2,\cdots,X_n\)，其观察值为\(x_1,x_2,\cdots,x_n\)，则称事件\(\{X_1=x_1,X_2=x_2,\cdots,X_n=x_n\}\)发生概率为：

\[ \begin{aligned} L(\theta) &= P(X_1=x_1,X_2=x_2,\cdots,X_n=x_n)\\ &= p(x_1;\theta)p(x_2;\theta)\cdots p(x_n;\theta) \\ &= \prod^n_{i=1}p(x_i;\theta) \end{aligned} \]

我们称\(L(\theta)\)为似然函数，它是一个关于未知参数\(\theta\)的函数。其形式与样本联合分布律\(p(x_1,x_2,\cdots,X_n;\theta)\)相同，但两者含义不同。

基于最大似然法的思想，我们应该取一个\(\theta\)估计值\(\hat{\theta}\)，使得\(L(\theta)\)取到最大，于是\(\hat{\theta}\)需满足：

\[ L(\hat{\theta}) = L(\hat{\theta};x_1,x_2,\cdots,x_n) = \max_{\theta\in\Theta}L(\theta;x_1,x_2,\cdots,x_n) \]

由此获得的\(\hat{\theta}_L=\hat{\theta}(x_1,x_2,\cdots,x_n)\)称为参数\(\theta\)的最大似然估计，相应的统计量\(\hat{\theta}(X_1,X_2,\cdots,X_n)\)称为\(\theta\)的极大似然估计量。

当X为连续型随机变量时，密度函数为\(f(x;\theta)\)似然函数的定义与离散型类似：

\[ L(\theta) = L(\theta;x_1,x_2,\cdots,x_n) = \prod^n_{i=1}f(x_i;\theta) \]

其余形式均与离散型类似，不过多赘述。

寻找极大似然估计常采用微分法：

\[ \left.\frac{{\rm d}L(\theta)}{{\rm d}\theta}\right|_{\theta=\hat{\theta}} = 0 \]

上式我们称为似然方程，鉴于我们比较关心极大值点而非极大值，为了计算方便，我们通常会取一个对数：

\[ l(\theta) = \ln L(\theta) = \sum^n_{i=1}\ln f(x_i;\theta) \]

称\(l(\theta)\)为对数似然函数，则似然方程等价于：

\[ \left.\frac{{\rm d}l(\theta)}{{\rm d}\theta}\right|_{\theta=\hat{\theta}} = 0 \]

最大似然估计的解题步骤也分为三步：

1. 写出似然函数
2. 取对数
3. 求导取零点

特别地，当求导得到的导数永不为0的时候，需要借助最大似然估计的存在性来估计参数，也就是在题目背景成立的前提下求得极大值点。

Tip

泊松分布\(P(\lambda)\)中，\(\lambda\)的矩估计为\(\overline{X}\)。

正态分布\(N(\mu,\sigma^2)\)中，\(\mu\)的矩估计为\(\overline{X}\)，\(\sigma^2\)的矩估计为\(\displaystyle\frac{1}{n}\sum^n_{i=1}(X_i-\overline{X})^2\)。

7.2 估计量的评价标准

常用的评价标准有无偏性、有效性、均方误差和相合性。

7.2.1 无偏性准则

定义：若参数\(\theta\)的估计量\(\hat{\theta}=\hat{\theta}(X_1,X_2,\cdots,X_n)\)，满足\(E(\hat{\theta})=\theta\)，则称\(\hat{\theta}\)是\(\theta\)的一个无偏估计量。

• 若\(E(\hat{\theta})-\theta \neq 0\)，则称\(E(\hat{\theta})-\theta\)称为估计量\(\hat{\theta}\)的偏差。
• 若\(E(\hat{\theta})-\theta \neq 0\)，但满足\(\displaystyle\lim_{n\rightarrow +\infty}E(\hat{\theta}) = \theta\)，则称\(\hat{\theta}\)是\(\theta\)的渐进无偏估计。

如果我们的估计是有偏的，还可以通过纠偏来改善我们的估计：

假如\(E(\hat{\theta})=a\theta + b,\theta\in\Theta\)，其中\(\hat{\theta}\)是总体的有偏估计，那么\(\displaystyle\frac{\hat{\theta}-b}{a}\)也为无偏估计。

7.2.2 有效性准则

定义：设\(\hat{\theta}_1,\hat{\theta}_2\)是\(\theta\)的两个无偏估计，如果\(Var(\hat{\theta}_1)<Var(\hat{\theta}_2)\)，则称\(\hat{\theta}_1\)比\(\hat{\theta}_2\)有效。

7.2.3 均方误差准则

定义：设\(\hat{\theta}\)是参数\(\theta\)的点估计，方差存在，则称\(E[(\hat{\theta}-\theta)^2]\)是估计量的均方误差，记为\(Mse(\hat{\theta})\)，即：

\[ Mse(\hat{\theta}) = E[(\hat{\theta}-\theta)^2] \]

如果\(Mse(\hat{\theta}_1)<Mse(\hat{\theta}_2)\)，则称\(\hat{\theta}_1\)优于\(\hat{\theta}_2\)。

由定义，当\(\hat{\theta}\)为\(\theta\)的无偏估计时：

\[ Mse(\hat{\theta}) = Var(\hat{\theta}) \]

Tip

均方误差准则不需要估计是无偏估计，而有效性原则要求是无偏估计。

7.2.4 相合性准则

前面三种准则都在固定的样本容量下讨论，是在n一定的时候，不同的估计量对总体的代表性与稳定性。

但在实际运用中，我们也会想到，如果我们尽可能提高样本量，是否可以得到一个更加精确的估计值呢？

所以我们提出了相合性准则，用来描述一种估计方法得出的估计量随着样本量n的增长，是否会变得更加精确。

定义：设\(\hat{\theta}(X_1,\cdots,X_n\)为参数\(\theta\)的估计量，若对于任意的\(\theta\in\Theta\)，当\(n\rightarrow+\infty\)时，\(\hat{\theta}_n\)依概率收敛于\(\theta\)，即\(\forall\varepsilon>0\)，有：

\[ \lim_{n\rightarrow+\infty}P\left\{\left|\hat{\theta}-\theta\right|<\varepsilon\right\} = 1 \]

则称\(\hat{\theta}_n\)是\(\theta\)的相合估计量。

对估计参数的相合性证明，我们一般通过大数定律、切比雪夫不等式或者直接从定义入手。

7.3 区间估计

点估计是由样本对总体参数\(\theta\)进行的一个估计\(\hat{\theta}\)，但是现实中估计往往有一定随机性，不会恰好反应现实，为了反应这个近似值的误差范围，给出一个可靠程度，我们提出双侧区间估计法。

假设\((X_1, X_2, \cdots)\)是总体\(X\)的一个样本，双侧区间估计的方法是给出两个统计量：

\[ \hat{\theta}_1 = \theta_1(X_1, X_2, \cdots),\qquad\hat{\theta}_2 = \theta_2(X_1, X_2, \cdots) \]

使得区间\([\hat{\theta}_1, \hat{\theta}_2]\)以一定可靠程度盖住\(\hat{\theta}\)。

7.3.1 置信区间定义

设总体\(X\)的分布函数\(F(x;\theta)\)含有未知参数\(\theta\)，从中抽取样本\((X_1, X_2, \cdots, X_n)\)，对于给定的值\(\alpha(0<\alpha<1)\)，设有\(\hat{\theta}_1(X_1, X_2, \cdots, X_n)\)和\(\hat{\theta}_2(X_1, X_2, \cdots, X_n)\)两个统计量，使得

\[ P\left\{\hat{\theta}_1 < \theta < \hat{\theta}_2\right\} = 1-\alpha,\qquad\forall\theta\in\Theta \]

则称区间\([\hat{\theta}_1, \hat{\theta}_2]\)为参数\(\theta\)的双侧置信区间，\(1-\alpha\)为置信度。其中\(\hat{\theta_1}\)为双侧置信下限，\(\hat{\theta_2}\)为双侧置信上限。

置信区间的形象含义是，假如对同一个总体抽样100次，每次抽样的样本容量n相同，每个样本值确定一个置信区间\([\hat{\theta}_1, \hat{\theta}_2]\)，那么在100个置信区间中，由伯努利大数定律，约有\(1-\alpha\)的置信区间包含了真实的参数\(\theta\)。

当\(\alpha = 0.05\)，即置信水平为95%时，称为95%置信区间，随机区间包含真值\(\theta\)的概率为95%。

接下来我们明确几个概念：

• 置信区间长度： 称置信区间\([\hat{\theta}_1, \hat{\theta}_2]\)的平均长度\(L = E(\hat{\theta}_2 - \hat{\theta}_1)\)为区间的精确度。
• 误差限：称\(\displaystyle\frac{E(\hat{\theta}_1 - \hat{\theta}_2)}{2}\)为置信区间的误差限。

7.3.2 单侧置信限

由以上定义，若有

\[ P\left\{\hat{\theta}_1(X_1,X_2,\cdots,X_n)< \theta\right\} = 1-\alpha,\qquad\forall\theta\in\Theta \]

则称\(\hat{\theta}_1\)为参数\(\theta\)置信水平为\(1-\alpha\)的单侧置信上限，反之则为单侧置信下限。

7.3.3 枢轴量法

既然我们知道了置信区间的定义，那我们该如何求解一个参数的置信区间呢？其中一种方法是枢轴量法，介绍如下：

枢轴量的定义为：

设总体有概率密度（或概率分布律）\(f(x,\theta)\)，其中\(\theta\)是待估的未知参数，并设\(X_1,X_2,\cdots,X_n\)是来自该总体\(X\)的样本，如果样本和未知参数\(\theta\)的函数\(G(X_1,X_2,\cdots,X_n;\theta)\)的分布不依赖于未知参数，且完全已知，则称它为枢轴量。

我们可以根据以下三步来寻找\(\theta\)的置信区间：

1. 根据得到的样本构造函数\(G(X_1,X_2,\cdots,X_n)\)，使其含有待估参数\(\theta\)，含有待估参数的点估计，含有总体已知信息，分布不依赖于\(\theta\)以外的未知参数，并且分布已知。
2. 运用奈曼原则。对于给定的置信度\(1-\alpha\)，确定尽可能大的\(a\)，尽可能小的\(b\)，使得\(P\left\{a < G(\theta) < b\right\} \geq 1-\alpha\)。
   注：求双侧置信区间时，a和b分别是相应分布的\(\displaystyle 1-\frac{\alpha}{2}\)和\(\displaystyle\frac{\alpha}{2}\)分位数，但这种估计对非对称分布的情况不是最优解，但在大多数情况中依然足够。

3. 等价变换。若能从\(a<G(\theta)<b\)得到等价不等式

   $$ \hat{\theta}_1 = \theta_1(X_1,X_2,\cdots,X_n) < \theta <\theta_2(X_1,X_2,\cdots,X_n) = \hat{\theta}_2$$

   那么，\((\hat{\theta}_1,\hat{\theta}_2)\)即为\(\theta\)的置信区,\(1-\alpha\)为置信度。

特别地，当求单侧置信限时候，只需要满足一侧取值即可，另一侧则趋于无穷。

7.4 正态总体参数的区间估计

7.4.1 单个正态总体的情形

\(X_2,X_2,\cdots,X_n\)为来自\(X\)的样本，\(\overline{X}\)和\(S^2\)分别为样本均值和方差，置信度为\(1-\alpha\)。

在单个正态总体下，常用的枢轴量有：

1. 总体\(\sigma^2\)已知时，估计\(\mu\)：\(\displaystyle\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\sim N(0,1)\)
2. 总体\(\sigma^2\)未知时，估计\(\mu\)：\(\displaystyle\frac{\overline{X}-\mu}{S/\sqrt{n}}\sim t(n-1)\)

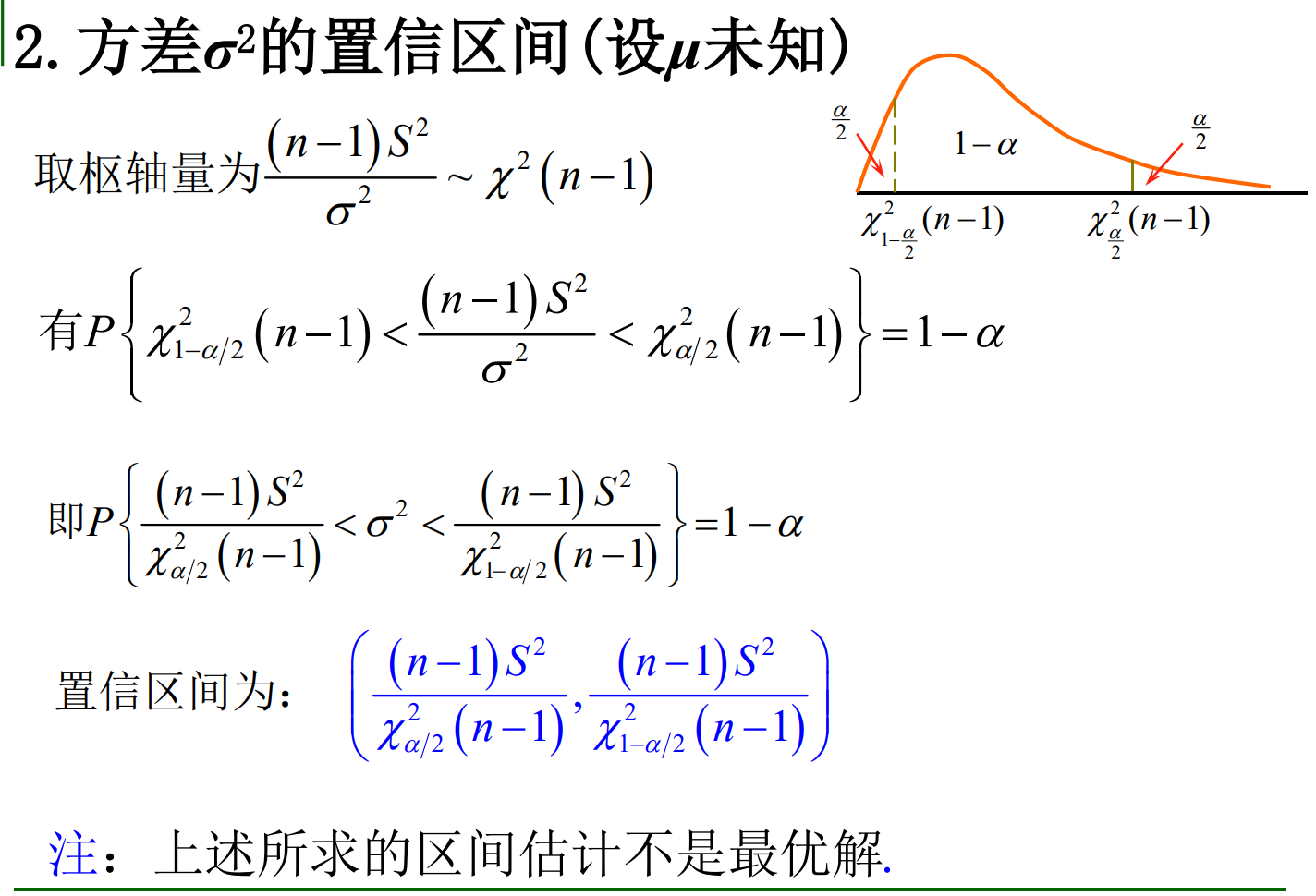
3. 总体\(\mu\)未知时，估计\(\sigma^2\)：\(\displaystyle\frac{(n-1)S^2}{\sigma^2}\sim \chi^2(n-1)\)

4. *总体\(\mu\)已知时，估计\(\sigma^2\)：\(\displaystyle\frac{\displaystyle\sum^n_{i=1}(X_i - \mu)^2}{\sigma^2}\sim \chi^2(n)\)

7.4.1.1 均值μ的置信区间

当\(\sigma^2\)已知时,

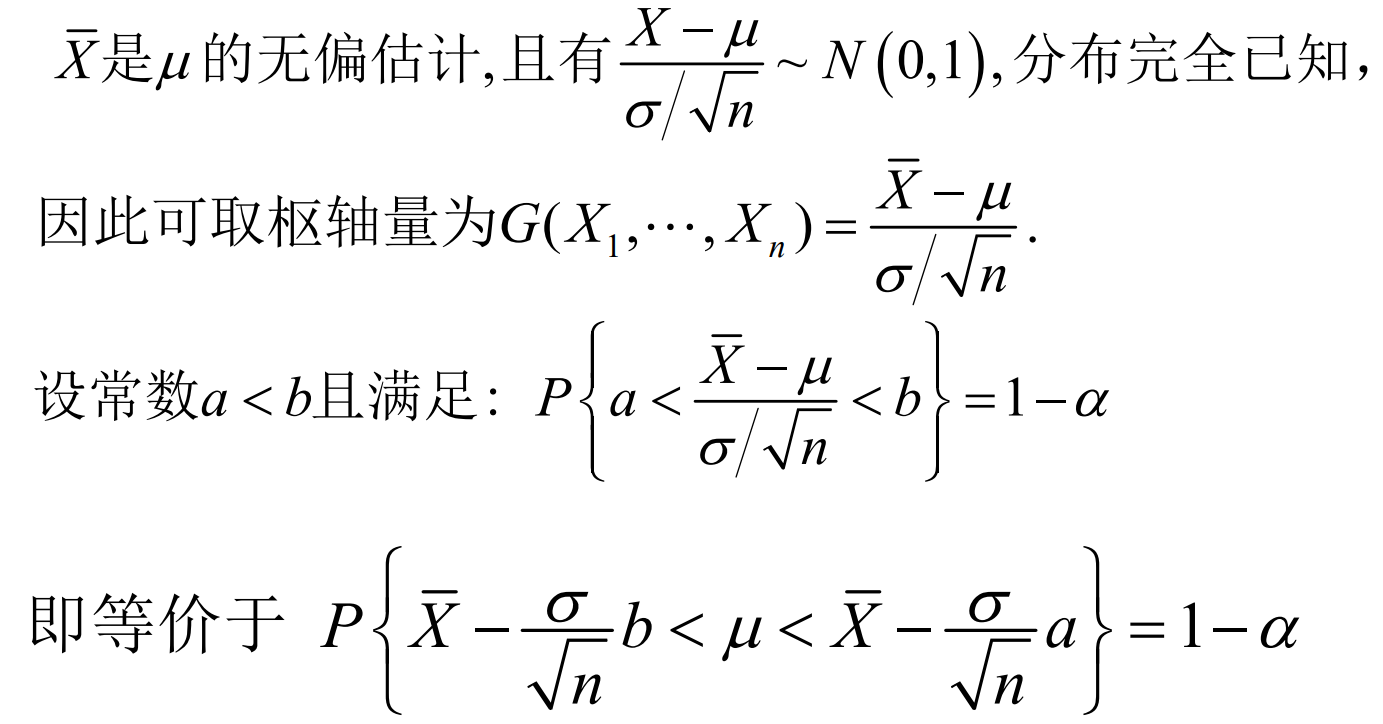
当\(\sigma^2\)未知时,

7.4.1.2 方差σ^2的置信区间

当\(\mu\)未知时，

7.4.1.3 成对数据的置信区间

在现实中常常遇到\(X，Y\)两组多次试验得到的成对数据，由于多次试验的结果之间不一定是同分布，且某次试验内成对数据也不一定独立，我们通常采用：

\[ D_i = X_i - Y_i,\quad i=1,2,\cdots,n \]

这样\(D_i, i=1,2,\cdots,n\)消除了同组内某些因素造成的差异，可以将\(D_1,\cdots,D_n\)独立同分布，为\(N(\mu_D, \sigma_D^2)\)。

7.4.2 双正态总体的情形

设\(X_1,X_2,\cdots,X_n\)为来自正态总体\(X_1\sim N(\mu_1, \sigma^2_1)\)的样本，\(Y_1,Y_2,\cdots,Y_m\)为来自正态总体\(X_2\sim N(\mu_2, \sigma^2_2)\)的样本，\(\overline{X}\)和\(\overline{Y}\)分别为样本均值，\(S^2_X\)和\(S^2_Y\)分别为样本方差，置信度为\(1-\alpha\)。

以下我们讨论对均值差\(\mu_1-\mu_2\)和方差比\(\displaystyle\frac{\sigma_1}{\sigma_2}\)两者如何进行区间估计。

7.4.2.1 均值差的置信区间

以下分三种不同的情况讨论：

当\(\sigma^2_1\)和\(\sigma^2_2\)已知时，

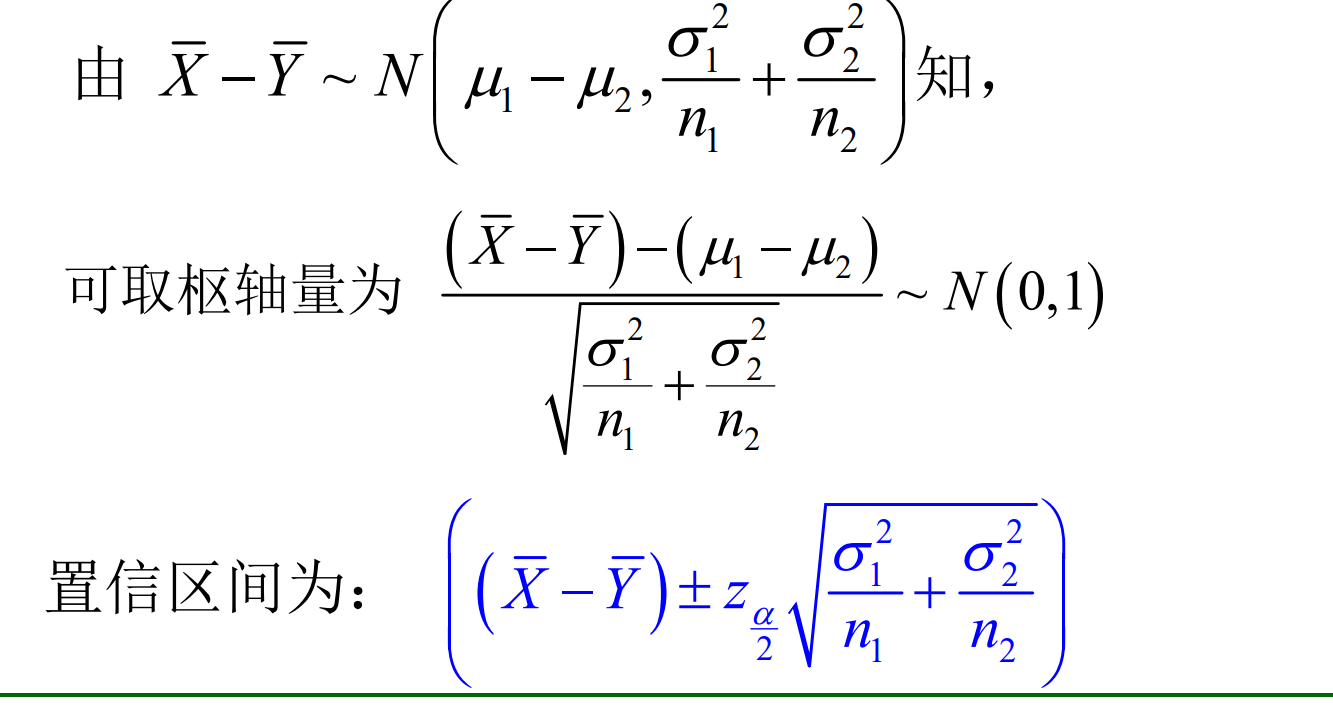
当\(\sigma^2_1 = \sigma^2_2 = \sigma^2\)，\(\sigma^2\)未知时，

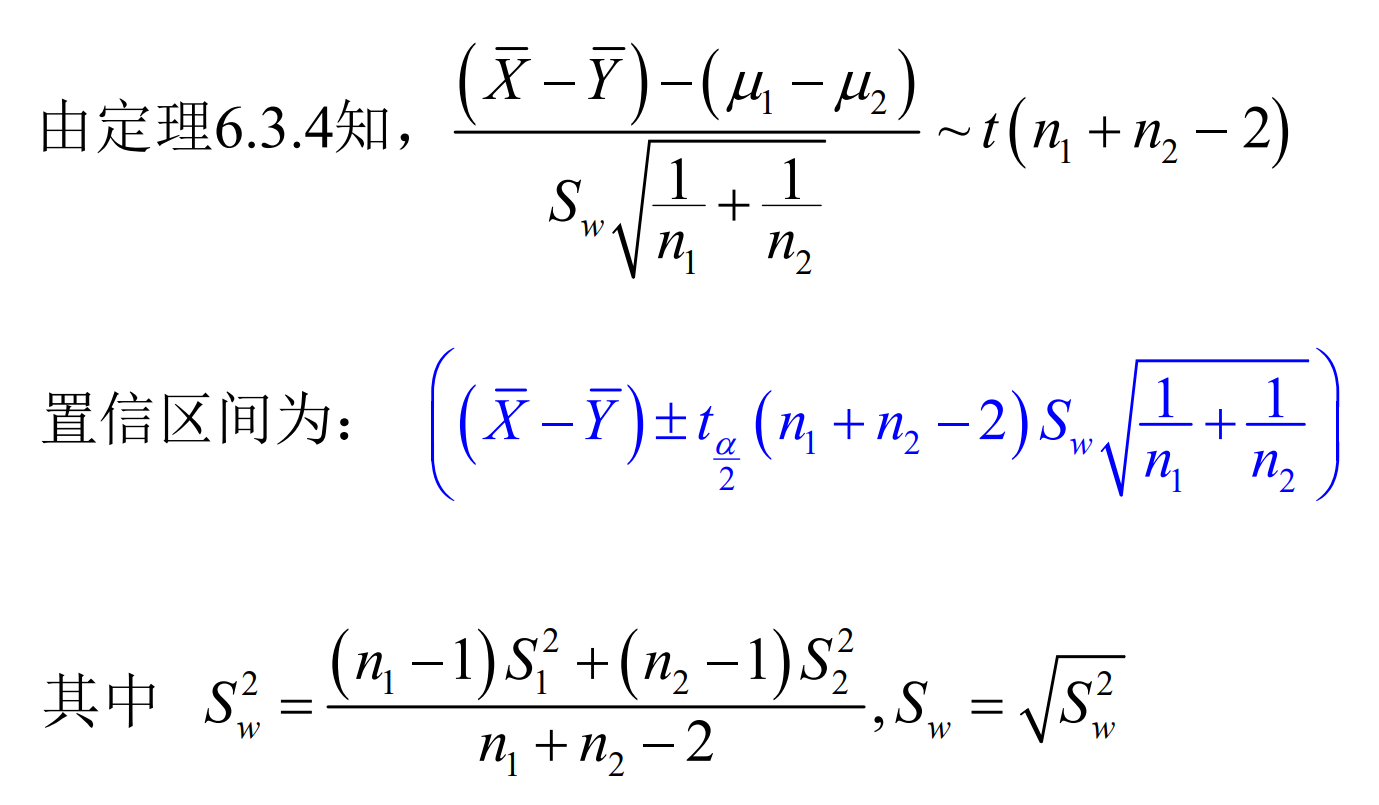
*当\(\sigma^2_1 \neq \sigma^2_2\)未知时，

对于有限小样本可以证明：

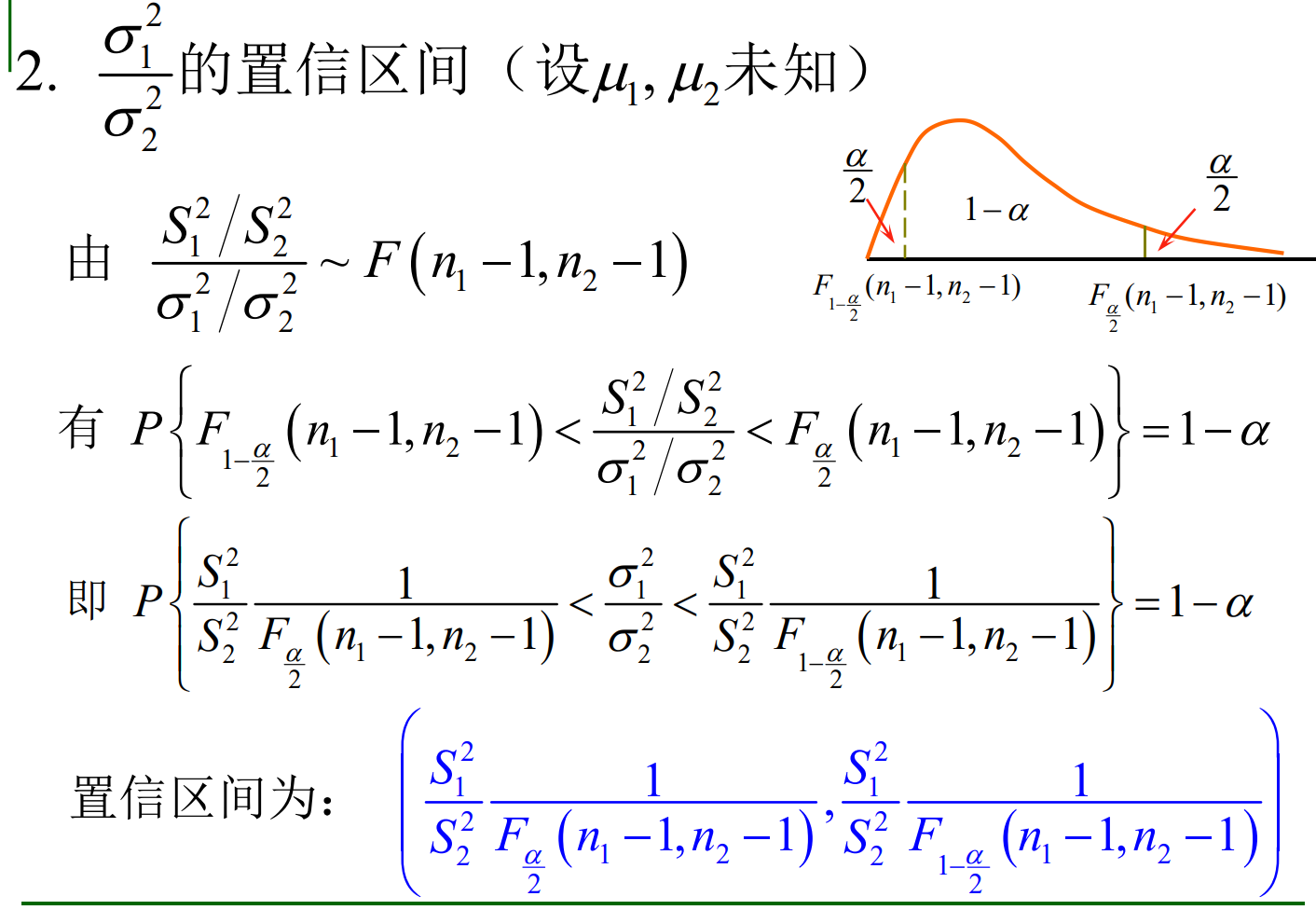
7.4.2.2 方差比的置信区间

当\(\mu_1\)和\(\mu_2\)未知时，

*7.5 非正态总体参数的区间估计

7.5.1 0-1分布参数的区间估计