电化学基础

约 2316 个字 预计阅读时间 8 分钟

3.1原电池

3.1.1 原电池构成与表示

我们从铜锌电池开始：
(假如我们有盐桥)

铜锌电池图示：

\[ (-)Zn\ |\ ZnSO_4(c_1)\ ||\ CuSO_4\ |\ Cu(+) \]

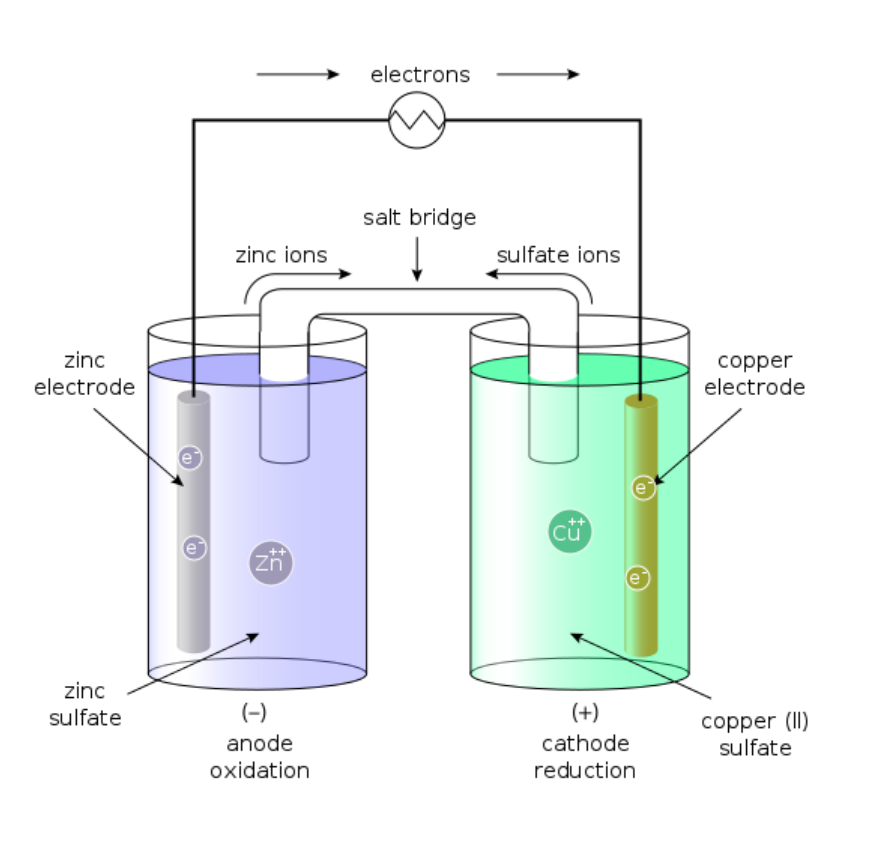
Tips:：
负极(阳极)写在左边, 正极(阴极)写在右边, 以双(虚)垂线"||"表示盐桥, 以单垂线"|"表示相界

更多示例：

\[ (-)Zn\ |\ H_2SO_4\ |\ Cu(+)\quad\quad{\footnotesize 伏打电池} \]

3.1.2 原电池电动势

对于电功：

\[ W_f=qE=nFE\\ \]

Tips:
\(其中F为法拉第常量\\ F=96485\ C·mol^{-1}\approx 96500\ C·mol^{-1}\)
\(n为发生1mol电池反应时电极通过电子的物质的量\)

对于自由能增量：

\[ \Delta_r G_m\leq-W_f \]

当电池反应可逆(即电流无限小)

\[ \Delta_r G_m=-W_f=-nFE \]

\[ E={-\Delta_r G_m \over nF} \]

若原电池各个组分都处在标准状态下，电池的电动势记为\({E^\theta}\)，则

\[ E^\theta={-\Delta_r G^\theta _m \over nF} \]

进一步讨论电动势和反应组分浓度的关系，我们有化学反应：

\[ aA(aq) + bB(aq) \xlongequal{\quad} gG(aq) + dD(aq) \]

其自由能增量\(\Delta_r G _m\)为

\[\begin{aligned} \Delta_r G _m &= \Delta_r G^\theta _m + RT\ln\frac{[{c(G) \over c^\theta}]^g[{c(D) \over c^\theta}]^d}{[{c(A) \over c^\theta}]^a[{c(B) \over c^\theta}]^b} \end{aligned}\]

代入\(\Delta_r G_m=-nFE\)

\[\begin{aligned} nFE &= nFE^\theta - RT\ln\frac{[{c(G) \over c^\theta}]^g[{c(D) \over c^\theta}]^d}{[{c(A) \over c^\theta}]^a[{c(B) \over c^\theta}]^b}\\ \\ E &= E^\theta - {RT \over nF}\ln\frac{[{c(G) \over c^\theta}]^g[{c(D) \over c^\theta}]^d}{[{c(A) \over c^\theta}]^a[{c(B) \over c^\theta}]^b} \end{aligned}\]

\[ {电动势能斯特(Nernst)方程} \]

Tips:
+ \({E^\theta}\)是标准电动势（电池反应各组分处于标准状态的电池的电动势）

• 电池的电动势与各组分浓度有关。

• 同理于反应平衡常数，能斯特方程中不出现纯的凝聚态物质（如纯固体和纯液体等）的浓度，或者把它当做"1"。对于气体组分，能斯特方程中以 \({p/p^\theta}\) 代替。

3.2 电极和电动势

3.2.1 电极电动势的产生

电极电动势\((\varphi)\)：

双电层理论:
电极表面与溶液中零电势处的电势差是该电极的(绝对)电极电势

Tips:
1. 金属阳离子从电极上进入溶液，电子留在电极上； 2. 溶液中形成紧密层、扩散层(静电作用和热运动）； 3. 电势分布曲线：远离电极处为零电势，电极表面具有不为零的电势。

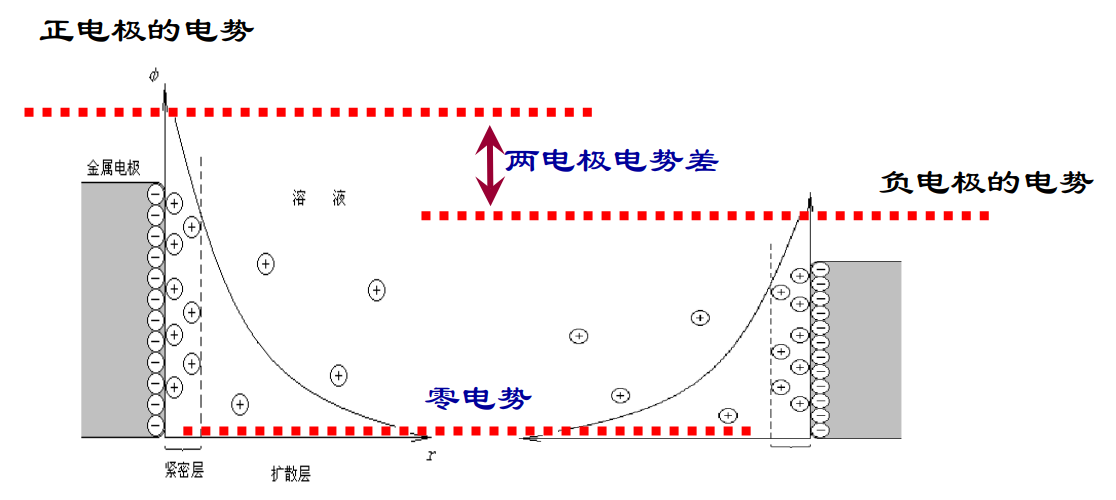
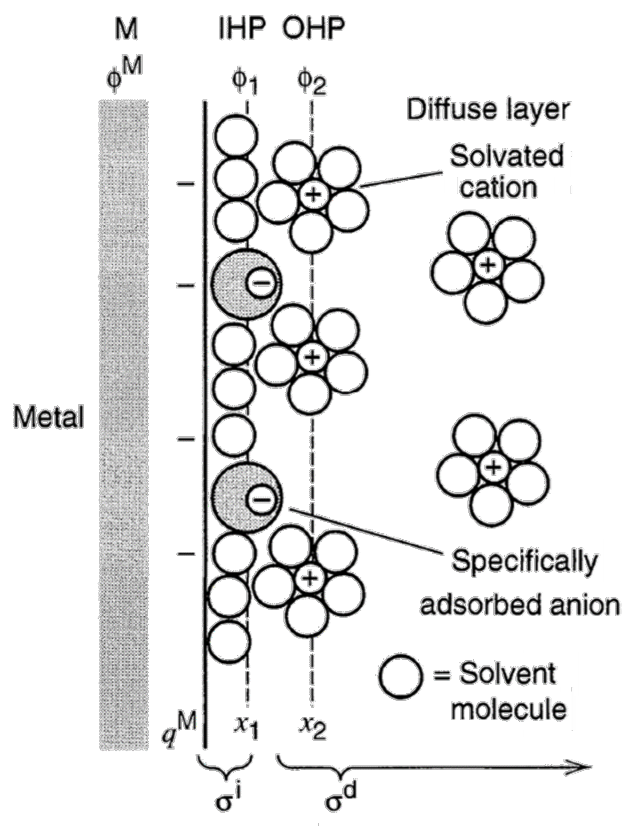
由于不同金属离子进入到不同溶液的能力不同，电极种类和溶液浓度都会对电极电势产生影响

电动势就是两电极的电势差： $$ E=\varphi(正极)-\varphi(负极) $$

3.2.2 相对电极电势

Tips:
电池由两个半电池组成，每个半电池都由一个氧化/还原对组成。（例如：\({Cu^{2+}/\ Cu}\)）

一个电极得氧化/还原对分别对应一个半反应，这个电极的其中一个半反应是：\({Cu - 2e^- \xlongequal{\quad}\ Cu^{2+}}{\quad\footnotesize （还原对上的半反应）}\)

应该指出的是，在特定的原电池中，一个电极只发生一个半反应，至于是氧化还是还原对，取决于其在原电池中充当正极还是负极。

电动势等于： $$ E=\varphi(正极)-\varphi(负极) $$

标准氢电极( SHE )：处于标准状态下的氢电极

\[ Pt\ |\ H_2 (p = p^\theta)\ |\ H^+\ (c = 1\ mol·L^{-1}) \]

即在\({c_{(H^+)}=1\ mol·L^{-1}}\)和\({p_{(H_2)}}=1\ atm\)的条件下，以用铂黑作为电极的体系称为标准氢电极。

Tips + \({1\ atm=101325\ kPa}\) + 铂黑电极是表面镀铂的铂电极，优点是表面积大 ，有利于氢气逸出。

电极反应式:

\[ 2H^+(1\ mol·L^{-1}) + 2e^- \longrightarrow H_2\ (100\ kPa) \]

将待测电极\({\rm (A^+/\ A)}\)与标准氢电极\({\rm (H^+/\ H)}\)组成原电池，规定标准氢电极电势为0，则该原电池电动势为待测电极电势的绝对值。
即：

\[ E=|\varphi^\theta(H^+/H_2)-\varphi(A^+/A)| \]

其中电极\({\rm (A^+/\ A)}\)的正负号确定，取决于其在测量时候发生的是氧化反应(正号"+")还是还原反应(负号"-")。

Tips:
对于确定的电极，其的电极电势不因为其发生的是氧化/还原反应而改变，因为其电极电势是参照标准氢电极比较的。

参比电极：甘汞电极

\[ Cl^-\ |\ Hg_2Cl_2(s)\ |\ Hg\\ \]

其电化学方程式： $$ {1 \over 2}Hg_2Cl_2 + e^- \longrightarrow Hg + Cl^- $$

3.2.3 电极电势的能斯特方程

电极电势的能斯特方程

有反应：

\[ aA+ne^-\underset{}{=\!=\!=}\ bB\\ \]

有能斯特方程：

\[ \varphi=\varphi^\theta-{RT \over nF}\ln{[{c(B) \over c^\theta}]^b \over [{c(A) \over c^\theta}]^a } \]

Tips:
上式中真数分子为还原态物质浓度(发生还原反应)，分母为氧化态物质浓度(发生氧化反应)

对于\({c/c^\theta}\)，若组分是纯固体/纯液体，则浓度取1；若组分是气体，则用\({p/p^\theta}\)代替。在前文有讨论过此点

Thinking:
联系以上公式，可以解答普化实验中为什么pH计在使用时候要设置温度。

下举一个例题说明能斯特方程的运用：

电极电势与电动势的关系：

对于标准氢电极与Ag电极组成的原电池：

\[ Pt\ |\ H_2(p^\theta)\ |\ H^+(c_{(H^+)}=1\ mol·L^{-1})\ ||\ Ag^+(c)\ |\ Ag \]

有电池反应式：

\[ {1 \over 2}H_2(p^\theta) + Ag^ + (c) \longrightarrow Ag(s) + H^+\ (c_{(H^+)}=1\ mol·L^{-1})\\ \]

\[ E = \varphi(Ag^+/Ag) = E^\theta - {RT \over F}\ln{{1 \over c_{Ag^+}}} \]

显然，在标准状态下：

\[ E = E^\theta = \varphi ^ \theta (Ag^+/Ag) \]

下举两道例题说明如何计算电极电势：

Tips：
+ 电池电动势是整个原电池所具有的电动势，其是由正负电极电势之差决定的

• 电极电势是电极自身在特定条件下所具有的电势，其取决于电极材料，溶液性质和温度等因素

• 电极电势可通过其所发生的半反应来计算，至于是氧化对还是还原对发生反应则不会影响计算结果。理由于此。

3.2.4 化学反应平衡常数的测定

我们观察化学热力学与电化学的两个重要公式：

\[ \begin{aligned} &\Delta_r G^\theta _m = -RT\ln{K^\theta}\\ &\Delta_r G^\theta _m = -nFE^\theta \end{aligned}\]

不难看出，\({K^\theta}\)与\({E^\theta}\)有关系如下：

\[ \ln{K^\theta}={nFE^\theta \over RT} \]

只要我们知道某一反应式的原电池形式下的标准电动势，就可以知道在特定温度下该反应的平衡常数，进而得到\({\Delta_r G^\theta _m}\)，\({\Delta_r H^\theta _m}\)，\({\Delta_r S^\theta _m}\)。

\[ E^\theta\Longrightarrow K^\theta\Longrightarrow {\Delta_r G^\theta _m} \]

\[ {{\rm d}\ln K^\theta \over {\rm d}T} = {{\Delta_r H^\theta _m} \over RT^2}\\ \ \\ {\small 不同温度下K^\theta 或者E^\theta\Longrightarrow \Delta_r H^\theta _m , \ \Delta_r S^\theta _m} \]

下给出两个例题，来说明以上推导如何运用：

3.2.5 拓展

3.2.5.1 离子选择电极

离子选择电极是专门用来测量溶液中某种特定离子浓度的指示电极。其中的一个例子就是在普化实验中用到的玻璃电极。

Tips：
玻璃电极作为测量pH的电极可看作是\({H^+}\)离子选择电极的一个例子。若将玻璃成分改变一下，并加入一些\({Al_2O_3}\)，即玻璃的基本组成为\({Na_2O-A1_2O_3-SiO_2}\)，则能使玻璃电极的电势对其它阳离子，如：\({Na^+}\)，\({K^+}\)，\({NH_4^+}\)，\({Ag^+}\)，\({Tl^+}\)，\({Li^+}\)，\({Rb^+}\)，\({Cs+}\)等各种一价阳离子具有特殊的选择性，即电极电势与某特定离子的浓度有关。

测量溶液的pH值:

就是测量溶液中\({H^+}\)的浓度。用玻璃电极作为指示 电极、甘汞电极为参比电极，与待测溶液组成原电池:

\({\small 饱和甘汞电极\ ||\ 试样溶液\ |\ pH玻璃电极}\)

测量该电池的电动势，即可求得溶液中\({H^+}\)的浓度。

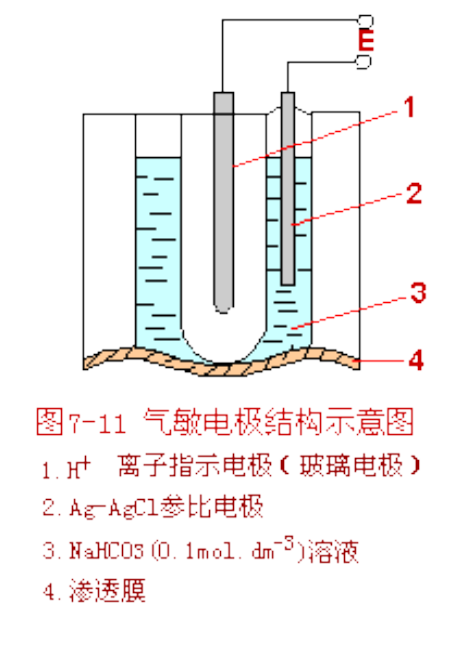
3.2.5.2 气敏电极

气敏电极是一种电化学气体传感器。它利用气敏电极或气体扩散电极测量混合气中或溶解在溶液中的某种气体的含量。其中典型的例子是\({CO_2}\)气敏电极。

3.3 电解池

由于本块内容在普通化学\({\mathrm{I}{\rm (H)}}\)中不作过的涉及，故附两张PPT仅作诠释：

3.4 本篇涉及公式速览

1. 对于电功：

\[ W_f=qE=nFE\\ \]

1. 对于自由能增量：

\[ \Delta_r G_m\leq-W_f \]

1. 对于电池电动势：

\[ E={-\Delta_r G_m \over nF} \]

1. 对于以下电化学方程式电动势计算：

\[ aA(aq) + bB(aq) \xlongequal{\quad} gG(aq) + dD(aq) \]

\[ E = E^\theta - {RT \over nF}\ln\frac{[{c(G) \over c^\theta}]^g[{c(D) \over c^\theta}]^d}{[{c(A) \over c^\theta}]^a[{c(B) \over c^\theta}]^b} \]

\[ {\footnotesize 电动势能斯特(Nernst)方程} \]

1. 电池电动势等于：

\[ E=\varphi(正极)-\varphi(负极) \]

1. 电极电动势能斯特方程：

\[ \varphi=\varphi^\theta-{RT \over nF}\ln{[{c(B) \over c^\theta}]^b \over [{c(A) \over c^\theta}]^a } \]

1. 电化学与热力学的联系： $$
   \begin{aligned} \Delta_r G^\theta _m &= -RT\ln{K^\theta}\ \Delta_r G^\theta _m &= -nFE^\theta\ \ln{K^\theta} &= {nFE^\theta \over RT}\ {{\rm d}\ln K^\theta \over {\rm d}T} &= {{\Delta_r H^\theta _m} \over RT^2} \end{aligned}$$

\[ \lim_{x \rightarrow \infty}\frac{\ln n}{\ln (\sqrt{n^2 + 1} + n)} \]