Skip to content

第四章 刚体力学

约 1637 个字 预计阅读时间 5 分钟

4.1 刚体运动的描述

刚体
刚体是一种特殊的质点系统；无论它在多大外力作用下，系统内任意两质点间的距离始终保持不变。

4.1.1 刚体的平动

平动
当刚体运动时，如果刚体内任何一条给定 的直线，在运动中始终保持它的方向不变，这种 运动叫平动。

对于刚体的平动，其位移相同，速度和加速度也相同。

由以上特点，我们可以将刚体平动简化为质心的（质点）运动。

4.1.2 刚体的定轴转动

刚体定轴运动
刚体上各点都绕同一转轴作不同半径的 圆周运动，且在相同时间内转过相同的角度

我们描述一个刚体的定轴转动，首先要将模型简化，对于一个定轴旋转的刚体，其垂直于转轴的平面称为转动平面，研究刚体的定轴转动可以简化为研究转动平面的定轴转动。

由右手螺旋定则：

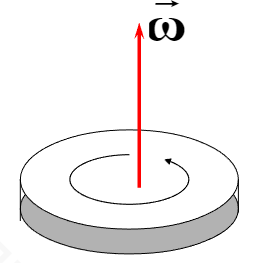
此处，我们模仿运动学，加入多个物理量：

  • 角位置\({\theta}\)
  • 角速度\({\vec{\omega}}\)
  • 角加速度\({\vec{\alpha}}\)

4.2 刚体的角动量与转动惯量

对于一个以Oz为轴做定轴转动的刚体，其对轴Oz的角动量等于其上各个质点的对轴Oz的角动量的矢量和：

此处简化，仅作大小上的探讨

\[\begin{aligned} L&=\sum_i(\Delta m_ir_iv)\\ &=(\sum_i \Delta m_ir_i^2)\omega\\ 所以，有&\\ \frac{{\rm d}L}{{\rm d}t}&=(\sum_i \Delta m_ir_i^2)\alpha\\ 得到&\\ M&=(\sum_i \Delta m_ir_i^2)\alpha \end{aligned} \]

我们令\({\displaystyle J=\sum_i \Delta m_ir_i^2}\)，所以我们有：

\[ M=J\alpha \]

其中\({J}\)称为转动惯量

同牛顿第二定律作对比，我们发现：

\[ \begin{aligned} &力矩M\longrightarrow 力F\\ &转动惯量J\longrightarrow 质量m\\ &角加速度\alpha\longrightarrow 加速度a \end{aligned} \]

转动和平动在运动学和动力学上都是存在联系的！

4.2.1 一维定轴转动

对于一维定轴转动，其必然涉及到沿转动体长度的积分

平行轴定理
对于一刚体，其质心为M，若其绕着任意一个与过质心转轴平行的转轴平行，两者相距d，刚体对其转动惯量为J，则有： \(\({J=J_C + md^2}\)\)

其中\({J_C}\)为过该质心转轴的转动惯量

由以上性质，我们知道对于一个刚体来说，其朝向某一方向的一堆转轴里，过质心的那个的转动惯量总是最小的。

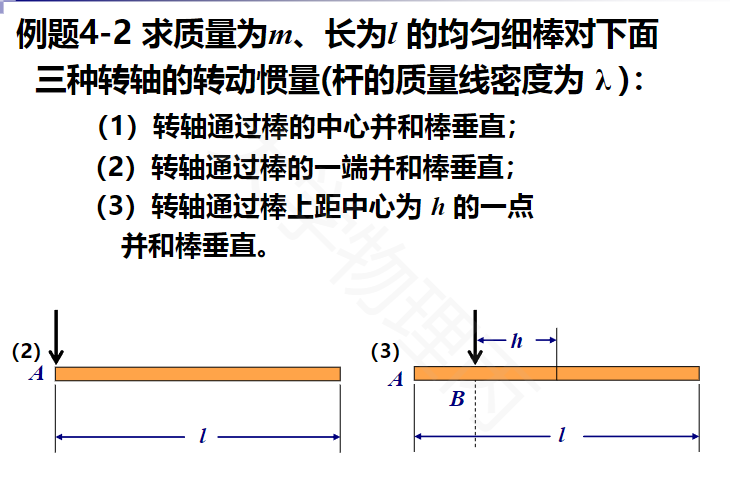
\[ \begin{aligned} &如图，取微元{\rm d}x，\\ &则有{\rm d}m=\lambda {\rm d}x(\lambda = m/l)\\ &\begin{aligned} 解：(1)\quad J_C&=\int r^2{\rm d}m\\ &=\int^{\frac{1}{2}}_{-\frac{1}{2}}x^2\lambda{\rm d}x\\ &=\lambda \frac{l^3}{12} \end{aligned}\\ &\begin{aligned} 因为\lambda l=m，代入得：J_C=\frac{1}{12}ml^2 \end{aligned} \end{aligned}\\ \]

剩下两道题留待证明。

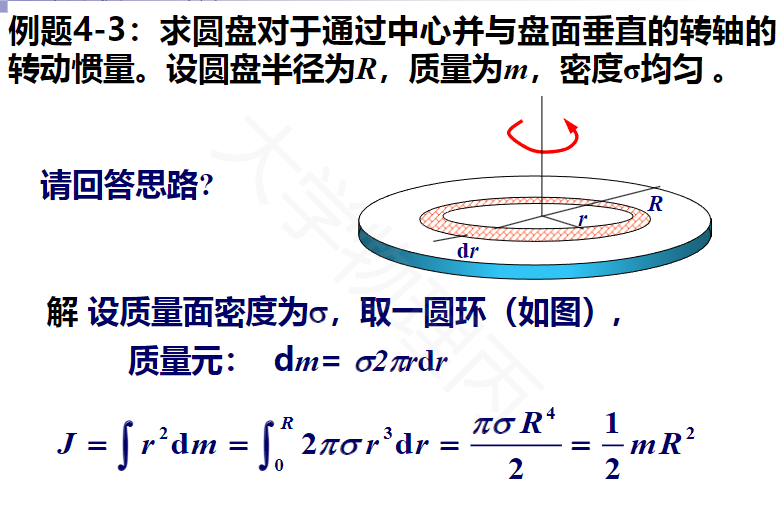
4.2.2 二维定轴转动

二维定轴转动里，特别为圆，涉及到对“环”的积分。

4.2.3 常用转动惯量

刚体 轴的位置 转动惯量
细圆环 通过圆心垂直于平面 \(MR^2\)
薄圆盘 通过圆心垂直于平面 \(\frac{1}{2}MR^2\)
沿直径 \(\frac{1}{4}MR^2\)
细棒 通过中点垂直于棒 \(\frac{1}{12}ML^2\)
通过端点垂直于棒 \(\frac{1}{3}ML^2\)
圆柱体 通过轴心 \(\frac{1}{2}MR^2\)
圆筒 通过轴心 \(\frac{1}{2}M(R_1^2+R_2^2)\)
球体 通过球心 \(\frac{2}{5}MR^2\)

4.3 刚体的定轴转动规律

一般而言，若施加在转动平面上的力不在转动平面时，有：

\[\begin{aligned} \vec{M}&=\vec{r}\times \vec{F}\\ &=\vec{r}\times(\vec{F}_1+\vec{F}_1)\\ &=\vec{r}\times\vec{F}_1+\vec{r}\times\vec{F}_2 \end{aligned} \]

其中\({\vec{F}_1}\)垂直于转动平面，\({\vec{F}_2}\)在平面内，由右手定则，前者的力矩垂直于转轴，后者的力矩平行于转轴。

值得注意的是，同平动不同的是，转动中的角动量是积累在转轴上。

所以仅有\({\vec{F}_2}\)对转动有作贡献，\({\vec{F}_1}\)在破坏转轴方向。

因此：

  • 力臂：对于力矩，我们有\({M_z=rF_2\sin\alpha = F_2d}\)，其中\({d=r\sin\alpha}\)称为力臂，是转轴到力作用线的距离
  • 方向：确定转轴后，可以沿着转轴确定+、-

4.3.1 刚体定轴转动定律

前文已有说明该重要公式：

\[ M=J\alpha=J\frac{{\rm d}\omega}{{\rm d}t} \]

上式中\({M}\)为合外力矩，为所有外力矩的矢量和。

同样值得注意的是，上式中\({M}\)的方向仅限于转动切向方向上，因为仅有此方向上对角动量有直接贡献作用。（其他方向的力需要对这个方向做正交分解）

\[ \begin{aligned} 对于m_2，有&:\\ &T_2 -m_2g=m_2a\\ 对于m_1，有&：\\ &m_1g-T_1=m_1a\\ 对于m，有&：\\ &M=\frac{1}{2}mR^2\alpha\\ 又因为M=&FR=(T_1-T_2)R\\ 联立上式，有&：\\ &\alpha=\frac{g}{R\alpha}·\frac{m_1-m_2}{\frac{1}{2}m+m_1+m_2} \end{aligned} \]

后面各种物理量自然容易推导，故此省略

4.3.2 刚体定轴转动的角动量定理

刚体的角动量定理
对刚体定轴转动，外力矩等于角动量对时间的变化率 \(\({M=\frac{{\rm d}L}{{\rm d}t}}\)\) 其中\({L=J\omega}\)为刚体的角动量

值得注意的是，对于刚体的角动量分析，可以将其转化为对多个分力产生的力矩的分析，最后取矢量和，形如下：

\[ M_z = \frac{{\rm d}L_z}{{\rm d}t}=\frac{{\rm d}}{{\rm d}t}\left(\sum_i J_i\omega_i\right) \]

不难看出其积分形式：

\[ \int_{t_0}^t M_z{\rm d}t=\sum_i J_i - \omega_i -\sum_i J_{0i}\omega_{0i} \]

角动量守恒定理
当外力矩为零时，角动量保持恒定 \(\({L=J\omega=常量}\)\) 当合外力矩为零时，系统的初末态满足： \(\({\sum_i J_i\omega_i=\sum_i J_{0i}\omega_{0i}}\)\)

4.4 小结

以下给出平动与转动之间的对比：

质点直线运动 刚体定轴转动
位移 \(x\) 角位移 \(\theta\)
速度 \(v=\frac{dx}{dt}\) 角速度 \(\omega=\frac{d\theta}{dt}\)
加速度 \(a=\frac{dv}{dt}\) 角加速度 \(\alpha=\frac{d\omega}{dt}\)
质量 \(m\) 转动惯量 \(J\)
力 \(F=ma\) 力矩 \(M=J\alpha\)
动量 \(p=mv\) 角动量 \(L=J\omega\)
动能 \(E_k=\frac{1}{2}mv^2\) 转动动能 \(E_k=\frac{1}{2}J\omega^2\)
冲量 \(I=F\Delta t=\Delta p\) 角冲量 \(I=M\Delta t=\Delta L\)
功 \(W=F\cdot x\) 功 \(W=M\cdot \theta\)
功率 \(P=F\cdot v\) 功率 \(P=M\cdot \omega\)