第七章 机械波
7.1 机械波的产生和传播
波动是振动的传播过程,机械波是机械振动在介质中的传播过程。
7.1.1 机械波产生的条件
波源——引起波动的最初开始振动的部分
媒介——传播波动的物质叫做煤质
7.1.2 横波和纵波
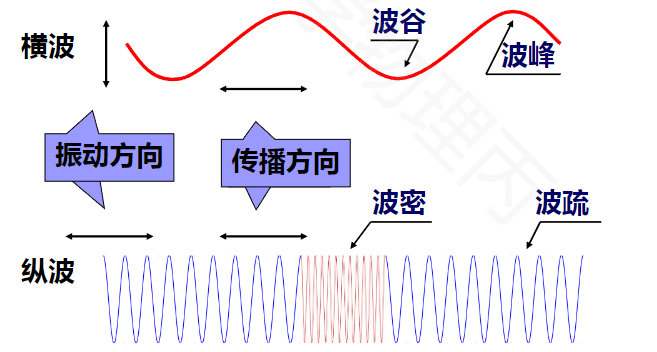
- 横波:质点的振动方向和波的传播方向垂直。
- 纵波:质点的振动方向和波的传播方向平行
两者波形示意如下:
7.1.3 波阵面和波射线
- 波阵面:振动相位相同的点连成的面(简称面)。
- 波前:在任何时刻,波面有无数多个,最前方的波面即是波前。波前只有一个
- 波线:沿波的传播方向作的一些带箭头的线。波线的指向表示波的传播方向。
波线和波阵面(波面)通常是垂直的。
根据波面的形状,波可以分为以下三种:
- 平面波:波面为平面
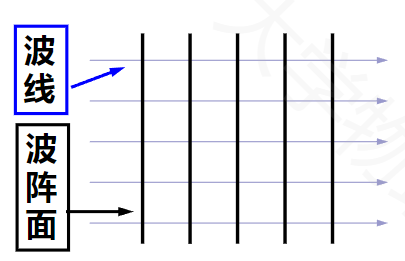
- 球面波:波面为球面
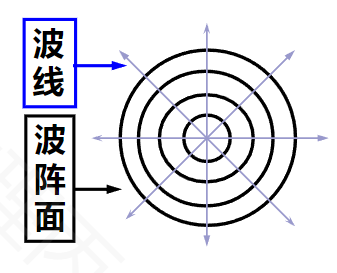
- 柱面波:波面为柱面
7.1.4 波的传播速度
波速
单位时间内一定的振动状态所传播的距离,用\(u\)表示。\(u\)的值通常取决于介质的弹性和质量密度
7.1.5 波长和频率
- 波长:在同一条波线上,相位差为\(2\pi\)的质点间的距离。
- 周期:传播一个波长距离所用的时间。
- 频率:周期的倒数。
其中,频率和周期只取决于波源,和介质种类无关。
波速、周期和波长之间存在如下关系:
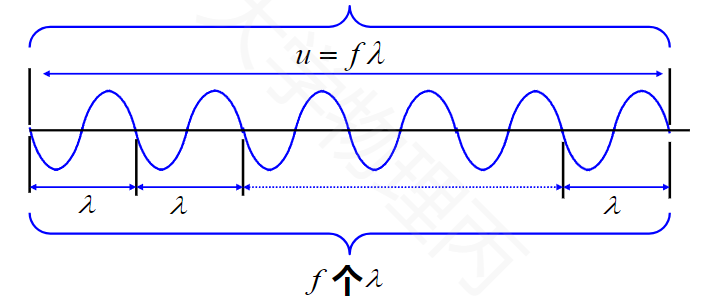
7.2 平面简谐波
7.2.1 平面简谐波的波动表达式
假设有一平面简谐波,在无吸收的均匀无限介中沿x轴的正方向传播,波速\(u\),取任意一条波线为x轴,取O点为轴原点,则O点处质点的振动表达式为:
7.4 波的叠加原理——波的干涉
7.4.1 惠更斯原理
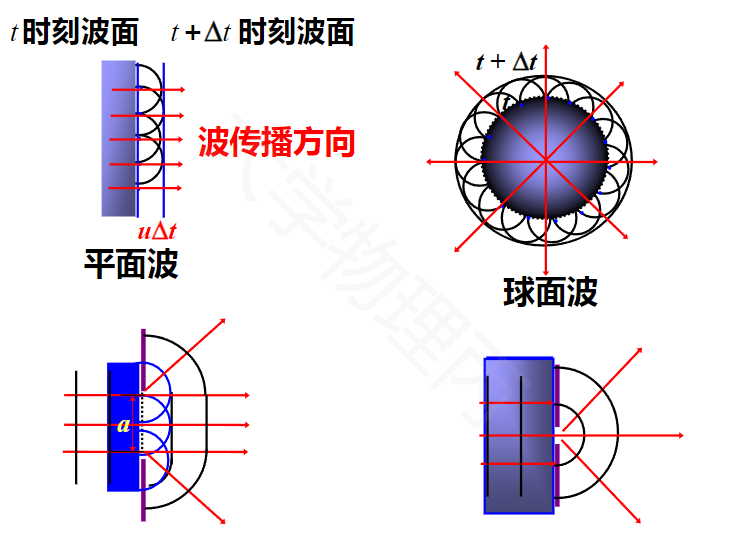
惠更斯原理
波动前沿上的每一点都可以看作是新的子波源,在某一时刻后的波前是由这些子波源发出的子波的包络面。
这个理论可以很好解释波的衍射和反射。
!
7.4.2 波的衍射
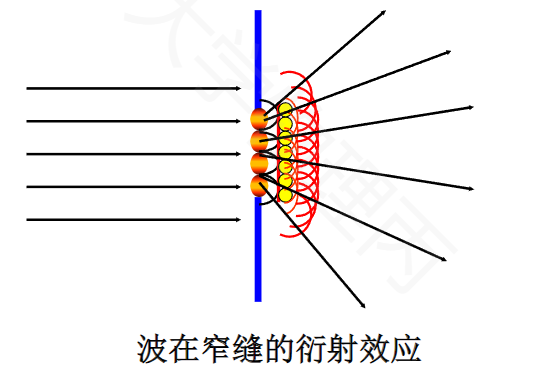
波的衍射
当波在传播过程中遇到障碍物时,其传播方向绕过障碍物发生偏折的现象,称为波的衍射
7.4.3 波的叠加
在了解波的干涉前,首先要了解波的两个性质:
波传播的独立性
两个或多个波在同一介质中同时传播时,各波的传播不受其他波的影响,各波的传播速度、频率和波长不变。波的叠加原理
两个或多个波同时传播时,各波的位移矢量在空间某点的代数和即为该点的合位移矢量。
7.4.4 波的干涉
相干波
相干波需要满足以下三个条件: + 振动方向相同 + 频率相同 + 相位相同/相位差恒定
相干波源:能发出相干波的波源称为相干波源。
我们接下来进行具体的讨论:
假设有两个相干波源\(S_1\)和\(S_2\),其距离\(P\)点分别为\(\overline{S_1P}\)和\(\overline{S_2P}\)。
那么两个相干波源的振动方程分别为:
由于波的传播独立性与叠加独立性,先研究两个波源在\(P\)点引起振动的方程:
S1在P点的振动方程为: $$ \begin{aligned} y_1 = A\cos(\omega t + \phi_{10} - \frac{2\pi r_1}{\lambda})\ y_2 = A\cos(\omega t + \phi_{20} - \frac{2\pi r_2}{\lambda}) \end{aligned} $$
合运动方程为:
在波的干涉中,存在一个重要的性质:波程差\(\delta = r_1 - r_2\)
两列相干波源为同相位时,在两列波的叠加的区域内,在波程差于零或等于波长的整数倍的各点,振幅最大;在波程差等于半波长的奇数倍的各点,振幅最小。
可见干涉条纹如下:
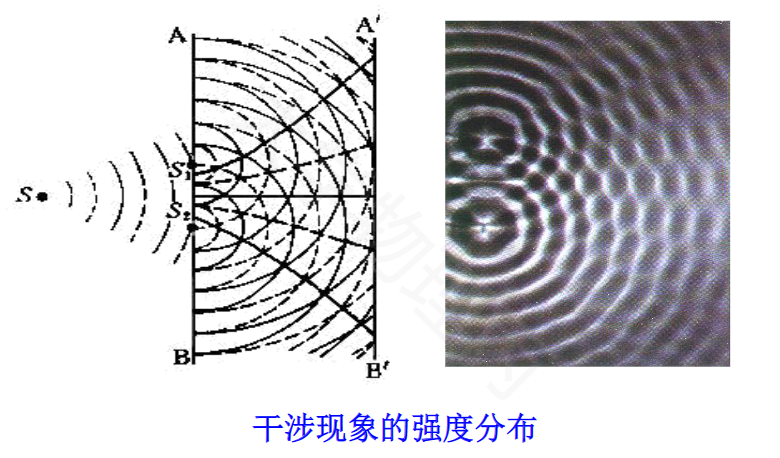
波的干涉
频率、同方向、相位差恒定的两列波,在相遇区域内,某些点处振动始终加强,另一些点处振动始终减弱
7.5 波的能量和能流密度
7.5.1 波的能量
<待补充>
7.5.2 平均能留密度
能流
单位时间内通过单位面积的能量
对于波来说,我们可以用平均能流密度衡量波的强度。
简单应用到波上,对于平面波来说,如果煤质不吸收能量,则振幅不变。
对于球面波来说,如果煤质不吸收能量,则振幅与距离呈反比
7.6 *驻波和多普勒效应
7.6.1 驻波及其产生
驻波
两列振幅、频率和振动方向都相同的相干波,沿相反方向传播时叠加而形成的一种特殊的干涉现象。
驻波方程为:
7.6.2 半波损失
半波损失
对于一个从波疏到波密介质传播的波,在波密与波疏介质的交界点上,反射波的相位落后入射波的相位\(\pi\)。