化学动力学基础
引言
第二章中探讨了化学热力学,主要关注的是平衡问题——化学反应向哪个方向进行?进行的程度如何?
本章讨论的是化学动力学,主要关注的是速率问题——化学反应进行的速率有多大?具体途径如何?
4.1 反应速率
有些反应在热力学上是极其有利的,但是在动力学上不一定有利于发生
4.1.1 反应速率定义
一般定义 \({\quad r = \pm{1 \over V}·{d_n \over d_t}}\)
常用定义 \({\quad r = {d_c \over d_t}}\)(当反应是恒容的时候)
最常用最直观的方法是对反应物消耗速率与生成物产生速率进行研究。我们有以下例子: $$ N_2 + 3H_2 \xlongequal{\quad} 2NH_3 $$
其中不难得出:
所以我们有规定,对于一个特定的反应,其速率方程等于某一物质的反应速率除以其的化学计量数;
4.2 反应动力学方程
Tips:
一般来说,反应动力学方程是在其他因素(如温度)固定不变时,定量描述浓度对反应速率影响的数学方程
4.2.1 基元反应的速率方程——质量作用定律
对于简单的气体反应(或者是基元反应): $$ {\rm \alpha A + \beta B \xlongequal{\quad} \gamma C} $$
不难看出\({r = k[A]^\alpha [B]^\beta\,}\)(碰撞理论)
对于分步完成的反应,比如反应\({A \xlongequal{} 2C}\)分两步完成:
- \({A \longrightarrow 2B\quad r_1 = k_1[A]}\)
- \({B \longrightarrow \,\,C\quad r_2 = k_2[B]}\)
由上述讨论我们发现: 质量作用定律仅适用于基元反应
4.2.2 反应级数和反应速率速率常数
反应动力学方程式可以是:
其中指数之和\(\alpha + \beta\)称为反应级数,\({k}\)是反应速率常数。
对于不是基元反应的化学反应,通常采用微分法(切线法),改变初始浓度法,尝试法三种方法测定反应的反应级数和反应速率常数。
4.3 简单级数反应的动力学方程
Tips:
速率方程:浓度对时间的一阶导数(一阶微分方程),展示的是反应速率和时间的关系。
积分形式:直观地表示浓度随时间变化(反应进程 )的关系式Attention!!!
本小节里所讨论的速率方程对不同的对象有不同的结果,对于反应物\({A,B}\)或者反应本身的速率方程都不一样,一定要注意区分!!!
4.3.1 零级反应
反应: \({A \longrightarrow P}\)
速率方程 \({\displaystyle\quad r_A = - {{\rm d}c_A \over {\rm d}t} = k}\)
进行以下推导:
其中\({B = c_{A_0}}\)
零级反应的半衰期为\({\displaystyle t_{1 \over 2} = \frac{c_{A_0}}{2k}}\)
Tips
零级反应特征:
- 反应物浓度~时间(\(c_A\)~\(t\))呈现直线关系,斜率为\({-k}\)
- 速率常数 k 的量纲:浓度\({·}\)时间\({^{-1}}\)
- 半衰期\({t_{1 \over 2}}\)与反应物起始浓度成正比,与速率常数成反比
零级反应的例子:
表面催化反应,光化学反应等等。
4.3.2 一级反应
反应:\({A \longrightarrow P}\)
速率方程 \({\displaystyle\quad r_A = - {{\rm d}c_A \over {\rm d}t} = kc_A}\)
进行以下推导:
其中\({B = \ln c_{A_0}}\)
由上式,对于一级反应半衰期推导如下:
当反应物\({c_A = {1 \over 2}c_{A_0}}\)时候,有
Tips:
一级反应特征:
- \({\ln{c_A}}\)与 \({t}\) 呈直线关系。
- 速率常数 k 的量纲:时间\({^{-1}}\),与浓度无关
- 半衰期与反应物起始浓度无关:\({t_{1 \over 2} = {\ln 2 \over k}}\)(这个特点很重要)
例:


4.3.3 二级反应
二级反应是我们在化学反应过程中最常见的反应类型,其包括了乙烯的二聚,碘化氢的热分解,乙酸乙酯的皂化反应等,包括了只包含一种反应物的二级反应和两种物质之间发生的二级反应。(有多种情况值得讨论)
4.3.3.1 一种物质的二级反应
反应:\({2A \longrightarrow P}\)
速率方程 \({\displaystyle\quad r_A = - {{\rm d}c_A \over {\rm d}t} = k_Ac_A^2}\)
进行以下推导:
其中\({B = \frac{1}{c_{A_0}}}\)
一种物质的二级反应的半衰期为\({\displaystyle t_{\frac{1}{2}} = \frac{1}{k_Ac_{A_0}}}\)
4.3.3.2 两种物质之间的二级反应
反应:\({A + B \longrightarrow P}\)
速率方程 \({\displaystyle\quad r_A = - {{\rm d}c_A \over {\rm d}t} = k_Ac_Ac_B }\)
由于这个方程中含有两个随时间变化的浓度,我们需要对反应方程进行进一步的探讨:
其中不难得出,\({\Delta c = r_A · t}\)
当\({t \rightarrow 0}\)时候,原本的速率方程可以转化为:
进行以下推导:
其中\({\displaystyle B = \frac{1}{c_{A_0} - c_{B_0}}\ln \frac{c_{A_0}}{c_{B_0}}}\)
带回原式中,有:
当我们的反应物\({A, B}\)起始浓度相同时候,有:
其中\({\displaystyle B = \frac{1}{c_{A_0}}}\)
此时计算其半衰期,为:\({\displaystyle t_{\frac{1}{2}} = \frac{1}{k_Ac_{A_0}}}\)
Tips:
二级反应特征:
- 当反应物只用一种,或者反应物起始浓度相同时候,\({\displaystyle\frac{1}{c_A}}\)与\({t}\)呈现直线关系。
- 速率常数的量纲为(浓度·时间)\({^{-1}}\)
- 当反应物只用一种,或者反应物起始浓度相同时候,二级反应的物质\({A}\)半衰期为\({\displaystyle t_{\frac{1}{2}} = \frac{1}{k_Ac_{A_0}}}\)
4.4 典型复合反应的动力学
4.4.1 平行反应
先讨论最简单的平行反应(如甲苯硝化)
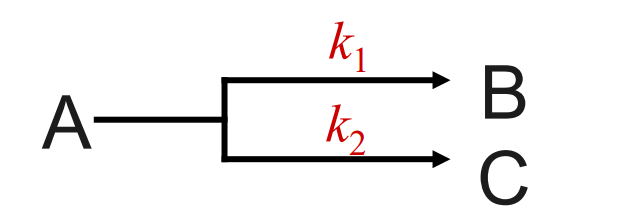
对于该反应流程,我们分析如下:
其中:
对上式积分,得:
Tips:
- 从上推导我们不难看出,在存在多个反应并行的反应——特别是有机反应中,同时发生的多个副反应,会使得产率降低。
- 对此我们可以采用合适的催化剂,来提高我们所希望发生的主反应的反应速率常数\({k}\),而催化剂针对某个\({k}\)的提升能力被我们称作催化剂的选择性,其对特定反应速率的提升,使得反应的选择性提高。
4.4.2 对行反应(即可逆反应)
典型对行反应:\({N_2 + 3H_2 \leftrightharpoons 2NH_3}\)
接下来我们讨论简单的对行反应:
对于上述反应,我们有:
正方向反应速率\({\quad r_{正} = k_1c_A}\)
反方向反应速率\({\quad r_{反} = k_{-1}c_B}\)
平衡常数\({\displaystyle\quad K = \frac{k_1}{k_{-1}}}\)
对于以上反应的净速率:
Tips:
对于典型对行反应——工业合成氨: $$ N_2 + 3H_2 \leftrightharpoons 2NH_3 \qquad \Delta H < 0 $$ 该反应为典型的放热对行反应,对于探求其最适于工业合成氨温度的问题,就是最佳反应温度问题——热力学和动力学的综合低温区:\({K}\)较大,\({k_1}\)为影响速率的主导因素,升高温度,速率增大;
高温区:\({\displaystyle\frac{1}{K}}\)逐渐上升为主导因素,升温会导致速率下降。由上,可见升温过程中反应速率会出现极大值,对应温度即为最佳反应温度。
4.4.3 连串反应
Tips:
本反应不要求特别掌握
我们有以下公式:
连串反应特征:
我们有线性非齐次方程如下:
对上式进行不定积分,有:
对其的积分过程详见最后连串反应线性非齐次方程积分详解
由上式定性分析,中间产物\({B}\)会出现一个极大值:
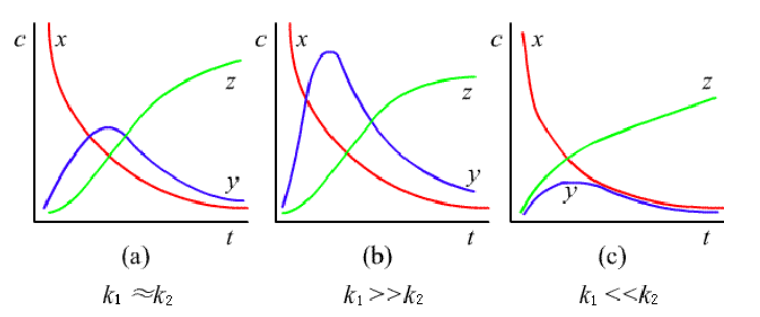
Tips:
对于以上对连串反应的讨论,理解配图是最重要的,因为这张图解释了接下来要讲的如何由上述反应机理来建立速率方程,可见平衡态法与稳定状态法
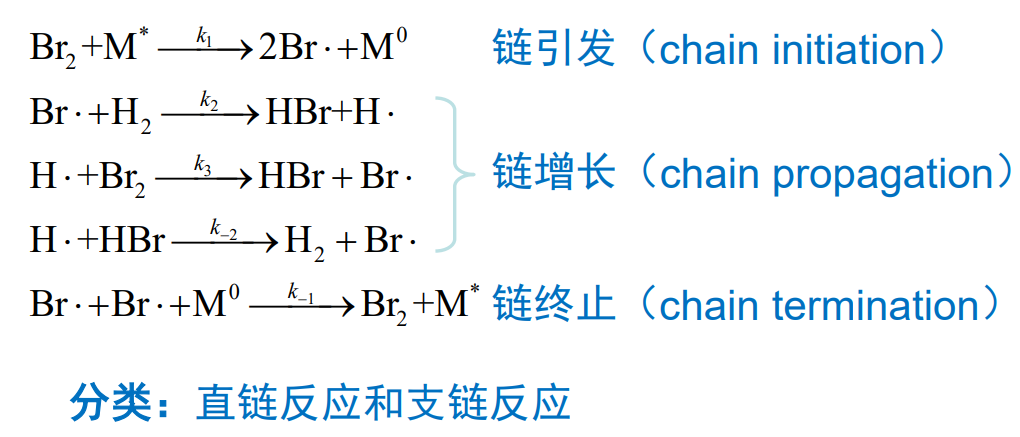
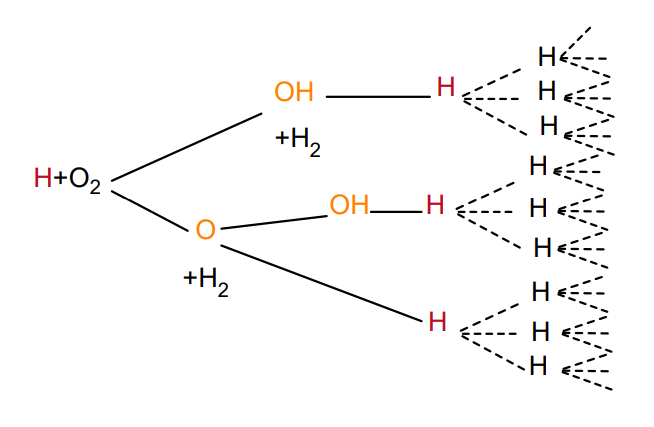
4.4.4 链反应
链反应由无限个基元反应组成,比如氢气的燃烧(支链反应),还有氢气与溴(直链反应)之间的反应:
直链反应:
支链反应:
4.4.5 由反应机理建立速率方程
Tips:
以上处理步骤是为了最终得到的速率方程中不出现难以测量或者度量的量,例如不稳定中间产物,不稳定自由基等等。
例:
其反应机理为:
其中\({I}\)是活泼中间物,按稳态处理:
下面以反应\({{\rm H_2 + Br_2 \longrightarrow 2HBr}}\)为例子具体说明:
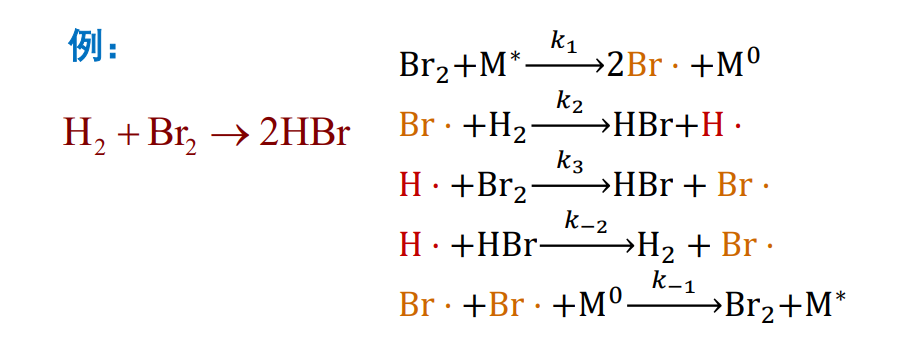
对于\({HBr}\)的生成速率:
在上述反应速率方程中\({\rm Br·}\)和\({\rm H·}\)为自由基,是活泼的,不稳定的中间物,需要消去。
对于\({\rm Br}\),应用稳定态法,我们有方程:
同理,对于\({\rm H}\),我们有:
上式相加,有:
会带入\({c_{\rm H}}\)速率方程中,我们有:
带回\({c_{\rm HBr}}\)的速率方程中,我们得到:
再有一道有机题目:
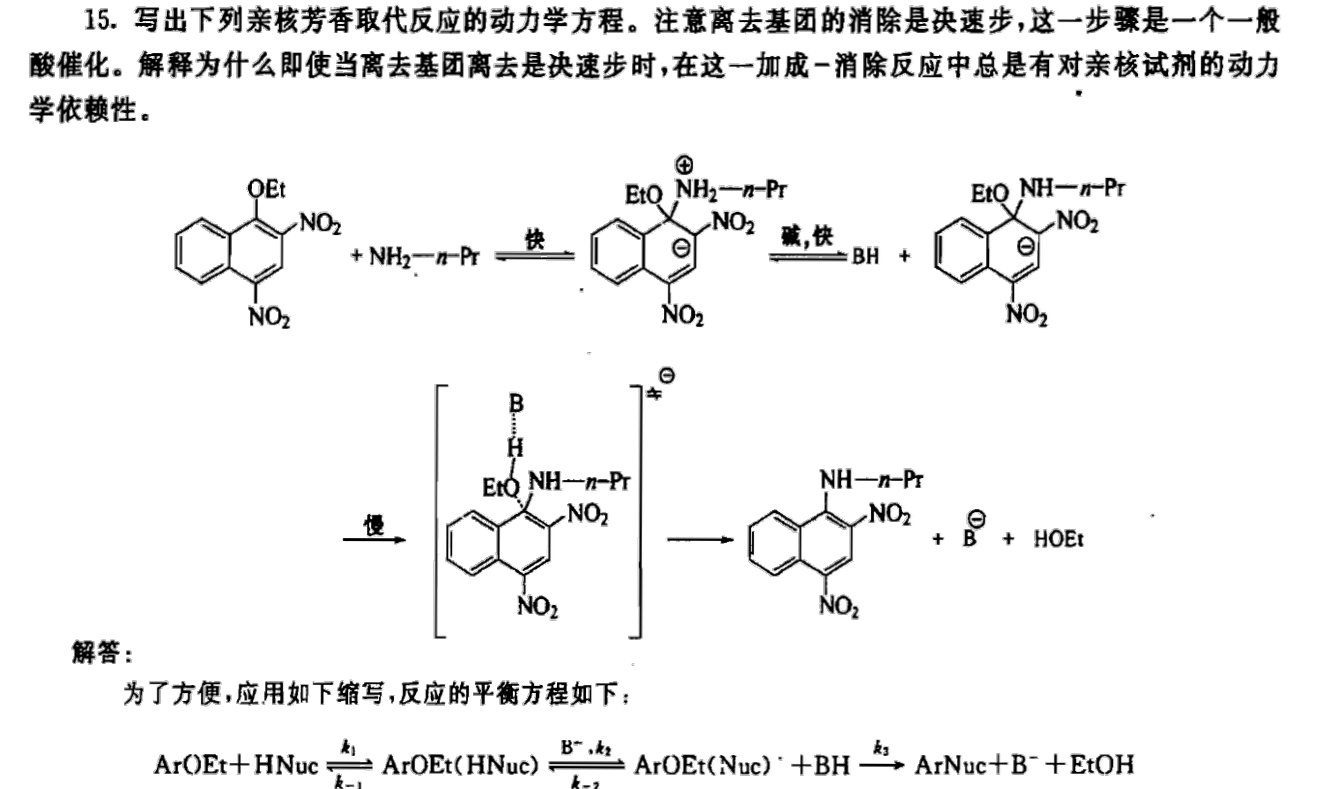


以上例子利用到了上文所提到的三个技巧。
4.4.6 酶催化动力学
米氏方程:\({\displaystyle v = \frac{V_{max}[S]}{K_m + [S]}}\) ,具体推导如下。
我们有酶\({E}\),底物\({S}\),酶与底物的结合物\({ES}\)以及产物\({P}\),他们存在以下反应历程:
我们有如下推导:
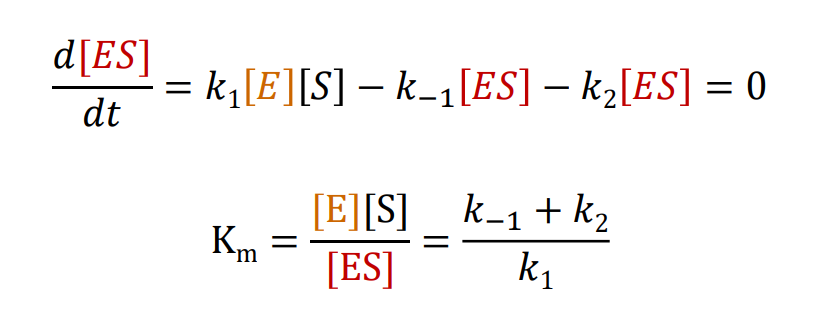

Tips:
米氏常数\({K_m}\)的物理意义:
- 米氏常数是反应速度为最大值一半时候的底物浓度,单位为\({mol/L}\)
- \({K_m}\)值表示酶与底物之间的亲和程度,越大亲和度越小,催化活性低,反之亦然。
有关于米氏常数的几点说明: + \({K_m}\)是酶的特征常数,与底物浓度,酶的浓度无关,与酶的特性,底物种类,\({pH}\),温度有关。 + 同一酶对于不同底物,\({K_m}\)最小的那个被称作最适底物
4.5 反应速率与温度的关系
4.5.1 碰撞理论
这是一个有关于解释分子间发生反应的理论。
Tips:
碰撞理论的要点:
- 单位时间内,分子间有效碰撞次数决定了反应速率,两者成正比
- 有效: 若碰撞分子动能达到了发生反应所需最低能量要求,并且碰撞方向正确,则称为一次有效碰撞,也就是发生反应的碰撞。
值得注意的是,一个体系中的分子的能量分布符合波兹曼分布(长得挺像正态分布的)
举一个具体的例子:
<待插入图片>
4.5.2 范霍夫近似规律
反应温度每提高\({\rm 10K}\),速率提高\({2 \sim 4}\)倍。
在工业上很多反应都需要加热,即使在这热力学上可能不利于其进行,但是有助于反应速率加快,配合分离技术来快速获得更多的产物。
4.5.3 阿伦尼乌斯方程
对于反应:
我们有经验式:
由于对于反应速率\({r}\)其与温度\({T}\)存在隐藏关系,经过实验验证,我们可以得到阿伦尼乌斯方程:
也可以表示为:
其中,\({E_a}\)称为反应的活化能,\({A}\)称为指前因子。显然,有\({A = e^B}\).
两侧同时对温度求导,有:
与\({\rm van't\ Hoff}\)方程很相似: <内容待补充> $$ \frac{{\rm d}\ln K}{{\rm d}T} = \frac{\Delta H_{vap}}{RT^2} $$
对两侧定积分,有:
最终我们得到:
Tips:
- 只有基元反应中,活化能\({E_a}\)的物理意义是明确的。
- 基元反应中,活化能\({E_a}\)最低者发生概率最大
- 对于整个反应所测量的实验活化能\({E_a}\)的物理意义是不明确的,只能视作多个基元反应活化能\({E'_a}\)的结合所产生的表现活化能
<联系合成氨反应待补充>
4.6 气固相界面反应的动力学
4.6.1 吸附现象
先讨论催化剂的分类: 1. 异相催化剂(化工生产使用最多) 2. 生物催化剂 3. 均相催化剂(用的最少)
Tips:
物理吸附和化学吸附:
- 物理吸附:活性炭等疏松多孔的结构
- 化学吸附: 气体分子与固体表面形成化学键的过程,等同于发生了化学反应。
- 存在单层吸附和多层吸附,并且吸附速率可以被反应速率表示。
- 吸附热力学:
\({\Delta G < 0\quad}\)自发反应过程(在吸附未满时候)
\({\Delta S < 0\quad}\)系统更加有序
\({\Delta H < 0\quad}\)焓变驱动的反应过程
4.6.2 吸附平衡
如果我们化学吸附这个过程看作一个化学反应(~~虽然它本来就是~~)
假设表面被覆盖的
4.6.3 表面反应动力学
被吸附在固体表面的分子发生化学反应,显然,其速率取决于在固体表面的浓度,可以用覆盖率\({\theta}\)表示固体表面浓度。
那么我们有: