第三章 多元随机变量及其分布
3.1 二元离散型随机变量
设\({E}\)是一个随机试验,样本空间\({S=\{e\}}\),设\({X=X(e)}\)和\({Y=Y(e)}\)是定义在\({S}\)上的随机变量,由它们构成的向量\({(X,Y)}\)叫做二元随机变量或二维随机变量。
3.1.1 联合概率分布
定义:若二元随机变量\({(X,Y)}\)全部可能取到的不同值是有限对或可列无限对,则称\({(X,Y)}\)是离散型随机变量。
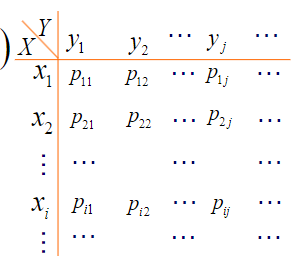
对于任意一种可能,表示为:
\[
P(X = x_i, Y = y_j) = p_{ij}
\]
联合概率分布有如下性质:
- 非负性:\({p_{ij}\geq 0}\)
- 归一性:\({\displaystyle\sum^\infty_{i=1}\sum^\infty_{j=1}p_{ij}=1}\)
3.1.2 边际分布
对于离散型随机变量\({(X,Y)}\),边际分布律为:
\[
\begin{aligned}
P(X=x_i)=\sum^\infty_{j=1}p_{ij}=p_{i·}\\
P(Y=y_j)=\sum^\infty_{i=1}p_{ij}=p_{j·}
\end{aligned}
\]
其中\({p_{i·}}\)表示\({p_{ij}}\)关于\({j}\)求和后得到的,\({p_{j·}}\)同理。
3.1.3 条件分布
对于离散型随机变量\({(X,Y)}\),当\({P(Y=y_j)>0}\)时,条件分布律为:
\[
P(X=x_i|Y=y_j)=\frac{P(X=x_i,Y=y_j)}{P(Y=y_j)}=\frac{p_{ij}}{\sum^\infty_{i=1}p_{ij}}
\]
同理,当\({P(X=x_i)>0}\)时:
\[
P(Y=y_j|X=x_i)=\frac{P(X=x_i,Y=y_j)}{P(X=x_i)}=\frac{p_{ij}}{\sum^\infty_{j=1}p_{ij}}
\]
结合边际分布,可知:
\[
P(X = x_i | Y = y_j) = \frac{P(X = x_i,Y = y_j)}{P(Y = y_j)} = \frac{p_{ij}}{p_{·j}}
\]
假如\({\{Y=y_j\}}\)固定,那么\({P(X = x_i | Y = y_j)}\)为在\({\{Y=y_j\}}\)条件下,随机变量\({X}\)的条件分布律。
反之亦然。
3.2 二元随机变量的分布函数
3.2.1 联合分布函数
定义,设\({(X,Y)}\)是二元随机变量,对于任意实数\({x,y}\),有二元函数\(F(x,y) = P\{(X\leq x) \cap (Y\leq y)\}\),记作:
\[
F(x,y) = P(X\leq x,Y\leq y)
\]
称为二元随机变量\((X, Y)\)的联合分布函数。
3.2.2 边际分布函数
对于二元随机变量\((X, Y)\),其边际分布函数为:
\[
\begin{aligned}
F_X(x) &= F(x,+\infty)\\
F_Y(y) &= F(+\infty,y)
\end{aligned}
\]
特别要注意的是,在实际的问题当中,对某一变量,求其边际分布函数,必须要保证另一变量要趋于无穷,也就是保证求和完全。
3.2.3 条件分布函数
对于二元随机变量\((X, Y)\),其条件分布函数为:
\[
\begin{aligned}
F_{X|Y}(x|y) &= P(X\leq x|Y=y)=\frac{P(X\leq x,Y=y)}{P(Y=y)}=\frac{F(x,y)}{F_Y(y)}\\
F_{Y|X}(y|x) &= P(Y\leq y|X=x)=\frac{P(X\leq x,Y\leq y)}{P(X\leq x)}=\frac{F(x,y)}{F_X(x)}
\end{aligned}
\]
3.3 二元连续型随机变量
3.3.1 联合概率密度函数
定义,对于二元随机变量\((X,Y)\)有分布函数\(F(X,Y)\),若存在非负函数\(f(x,y)\),对于任意实数\(x,y\),有:
\[
F(x,y) = \int^y_{-\infty}\int^x_{-\infty}f(u,v)dudv
\]
则称\(f(x,y)\)为二元随机变量\((X,Y)\)的联合概率密度函数,记作:
\[
f(x,y) = \frac{\partial^2F(x,y)}{\partial x\partial y}
\]
联合密度函数性质
- 非负性: \(f(x,y)\geq 0\)
- 归一性: \(\displaystyle\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f(x,y)dxdy=1\)
- 设\(D\)是xoy平面上的区域,点\((X,Y)\)落在\(D\)内的概率为:\(P((X,Y)\in D)=\displaystyle\underset{D}{\int\int}f(x,y)dxdy\)

积分该密度函数,先画图,再确定先积什么变量,将二重积分转化为两步积分。

\[
\begin{aligned}
解:(1)\quad 1 &= \int^\infty_{-\infty}\int^\infty_{-\infty}f(x,y)dxdy\\
&= \int^\infty_0\int^\infty_0ke^{-(2x+3y)}dxdy\\
&= k\int^\infty_0e^{-2x}dx\int^\infty_0e^{-3y}dy\\
\end{aligned}
\]
以上示例简单展示了如何处理二重积分。
3.3.2 二维连续随机变量的边际分布
对于二元随机变量\((X,Y)\),其边际分布函数为:
\[
\begin{aligned}
F_X(x) &= F(x,+\infty)\\
F_Y(y) &= F(+\infty,y)
\end{aligned}
\]
对于二元随机变量\((X,Y)\),其边际密度函数为:
\[
\begin{aligned}
f_X(x) &= \int^\infty_{-\infty}f(x,y)dy\\
f_Y(y) &= \int^\infty_{-\infty}f(x,y)dx
\end{aligned}
\]
3.3.3 条件概率密度
对于二元随机变量\((X,Y)\),其条件概率密度函数为:
\[
\begin{aligned}
f_{X|Y}(x|y) &= \frac{f(x,y)}{f_Y(y)}\\
f_{Y|X}(y|x) &= \frac{f(x,y)}{f_X(x)}
\end{aligned}
\]
3.3.4 二元均匀分布
定义,若二元随机变量\((X,Y)\)的联合概率密度函数为:
\[
f(x,y) = \begin{cases}
\frac{1}{S}, & (x,y)\in D\\
0, & \text{其他}
\end{cases}
\]
其中\(S\)为区域\(D\)的面积,则称其服从二元均匀分布。
记为:
\[
(X,Y)\sim U(D)
\]
3.3.5 二元正态分布
定义,若二元随机变量\((X,Y)\)的联合概率密度函数为:
\[
f(x,y) = \frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}\exp\left\{-\frac{1}{2(1-\rho^2)}\left[\frac{(x-\mu_1)^2}{\sigma^2_1}-2\rho\frac{(x-\mu_1)(y-\mu_2)}{\sigma_1\sigma_2}+\frac{(y-\mu_2)^2}{\sigma^2_2}\right]\right\}
\]
记为:
\[
(X,Y)\sim N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)
\]
值得注意的是,二维正态分布的两个边际分布都是一维正态分布,并且不依赖参数\(\rho\)。
二维正态分布的条件概率分布也是……一维正态分布!!!
下面做一个条件分布的总结:
条件分布函数:
\[
\begin{aligned}
F_{X|Y}(x|y) &= P(X\leq x|Y=y)\\
&=\begin{cases}
对于离散: \displaystyle\frac{P(X\leq x, Y=y)}{P(Y=y)}, & P(Y=y)>0\\
对于连续: \displaystyle\frac{\displaystyle\int_{-\infty}^x f(t,y)dt}{f_Y(y)}, & f_Y(y)>0\\
\end{cases}
\end{aligned}
\]
3.3.6 随机变量的独立性
定义:设\(F(x,y)\)及\(F_X(x),F_(Y)\)分别是二元随机变量\((X,Y)\)的联合分布函数,及边际函数,若有:
\[
F(x,y) = F_X(x)F_Y(y)
\]
则称\((X,Y)\)是独立的。
同样有其等价形式:
-
对于离散型:独立性等价于:
\[p_{ij} = p_ip_j\]
3.3.7 多元随机变量函数的分布
我们将上面的概念拓展,使用多元的变量来研究一个概率问题。
随机变量、分布函数、密度函数与边际分布函数都是类似的,故此不过多赘述。
3.4 二元随机变量的函数分布
如果有以下关系:
\[
\begin{aligned}
U &= u(X, Y)
\end{aligned}
\]
那么称\(F_U(u)\)为关于\((X, Y)\)的二元随机变量函数的概率分布。
基本的解题思路就是将变量还原为显式的函数表达,转化为已知的函数形式。
举一例子:
设二元连续型随机变量\((X, Y)\)具有概率分布\(f(x, y)\),且\(Z=g(X, Y)\)。问:\(Z\)的概率分布和密度函数是什么?
\[
\begin{aligned}
&\begin{aligned}
F_Z(z) &= P(Z \leq z)\\
&= P(g(X, Y) \leq z)\\
&= \underset{g(X, Y) \leq z}{\int\int}f(x,y){\rm d}x{\rm d}y\\
\end{aligned}\\
&\begin{aligned}
f_Z(z) = \left(F_Z(z)\right)'
\end{aligned}
\end{aligned}
\]
3.4.1 Z=X+Y分布
设\((X, Y)\)概率密度为\(f(X, Y)\),则\(Z=X+Y\)的分布函数为:
\[
\begin{aligned}
&\quad\begin{aligned}
F_Z(z) &= P(Z\leq z)\\
&= P(X+Y \leq z)\\
&= \underset{x+y\leq z}{\int\int}f(x, y){\rm d}x{\rm d}y\\
&= \int^{+\infty}_{-\infty}{\rm d}x\int^{z-x}_{-\infty}f(x, y){\rm d}y\\
\end{aligned}\\
&\begin{aligned}
令u=x+y,那么有
\end{aligned}\\
&\quad\begin{aligned}
原式 &= \int^{+\infty}_{-\infty}\left[\int^{z}_{-\infty}f(u-x, x){\rm d}u\right]{\rm d}x\\
&= \int^{z}_{-\infty}\left[\int^{+\infty}_{-\infty}f(u-x, x){\rm d}y\right]{\rm d}u\\
&=\int^{z}_{-\infty}f_Z(u){\rm d}u
\end{aligned}
\end{aligned}
\]
由上,不难看出\(f_Z(z) = \displaystyle\int^{+\infty}_{-\infty}f(z-x, x){\rm d}x\)
当X与Y相互独立的时候,有卷积公式:
\[
f_Z(z) = \int^{+\infty}_{-\infty}f_X(x)f_Y(z-x){\rm d}x
\]
对于泊松分布,可以证明,n个相互独立的服从泊松分布的随机变量的和依旧服从泊松分布,其参数为n个分布的参数之和,即\(\displaystyle Z\sim P(\sum^n_{i=1}\lambda_i)\)。
对于正态分布,可以证明,n个相互独立的服从正态分布的随机变量的和依旧服从正态分布,且若\(X_i\sim N(\mu_i, \sigma^2_i)\),那么有\(\displaystyle Z\sim N\left(\sum^n_{i=1}\mu_i, \sum^n_{i=1}\sigma^2_i\right)\)。
进一步可以证明,n个服从正态分布的随机变量的线性组合仍然服从正态分布。
3.4.2 max与min函数的分布
设\(X, Y\)是两个互相独立的随机变量,他们的分布函数分别为\(F_X(x)\)和\(F_Y(y)\),求\(M=max(X, Y)\)和\(N=min(X, Y)\)的分布函数。
\[
\begin{aligned}
&M = max(X,Y)的分布函数为:\\
&\begin{aligned}
F_{max}(z) &= P(M\leq z)\\
&= P(X\leq z, Y\leq z)\\
&= F(z, z)\\
&= F_X(z)·F_Y(z)
\end{aligned}\\
&N = min(X,Y)的分布函数为:\\
&\begin{aligned}
F_{min}(z) &= P(N\leq z)\\
&= P\{(X\leq z) \cup (Y\leq z)\}\\
&= F_X(z) + F_Y(z) - F_X(z)F_Y(z)\\
\end{aligned}\\
&或者有:\\
&\begin{aligned}
F_{min}(z) &= 1 - P(N > z)\\
&= 1 - P(X>z, Y>z)\\
&= 1 - P(X>z)·P(Y>z)\\
&= 1 - (1-F_X(z))(1-F_Y(z))
\end{aligned}\\
&上下两个式子等价
\end{aligned}
\]