第三章 对映异构
3.0 异构体分类
立体异构体
分子中原子或原子团互相连接的次序相同,但在空间的排列方向不同而引起的异构体对映异构体
两个化合物互为实物和镜像,但不能重合,因此是一对异构体,互为对映,称为对映异构体
3.1 分子的光学活性
3.1.1 物质旋光性
3.1.2 比旋光度
3.2 分子的对称性和手性
3.2.1 手性分子
3.2.2 对称因素
- 对称面
- 对称中心
- 对称轴
如果分子内存在对称面或对称中心,则其一定无手性,但若存在对称轴,分子有可能是手性分子
如何判断分子是否具有手性
- 分子镜像能否与实物重合
- 若不能重合,分子具有手性
- 操作较为繁琐
- 分子对称因素
- 分子内存在对称面或对称中心,则分子一定无手性
- 操作同样繁琐
- 检查分子是否含有手性碳原子
- 轴手性等特征
- 特殊情况:手性轴,可见后文
重要概念
- 手性分子也称为不对称分子
- 所有手性分子都具有对映异构体
- 手性分子通常具有旋光性,是旋光异构体
3.3 含有手性碳原子的化合物
手性分子的普遍因素——手性碳原子(连接四个不相同基团的碳原子
含有一个手性碳原子的分子一定是手性分子,有一对对映体,都具有旋光性,一个是左旋,一个是右旋。
3.3.1 对映异构体和外消旋体
对映异构体的部分物理性质:熔点、沸点、溶解度都相同;在非手性条件下反应的速度也相同。
在手性环境下,性质则不同。旋光方向相反,转过的角度相同。生理活性不同。(手性环境)
一对对映体等量混合得到外消旋体。其中外消旋体与单一对映异构体的物理性质性质不同:旋光度为0.
对映异构体的旋光性
使平面偏振光向右旋,称为右旋体;使平面偏振光向左旋,称为左旋体。二者旋转角度相同。因此对映异构也叫做旋光异构。
3.3.2 光学异构体构型表示方法
- 绝对构型表示法:R/S标记法
以下取自普通化学笔记:
> R-S标记法:
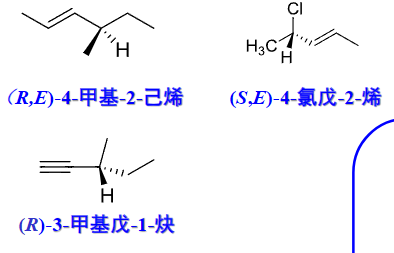
> 1. 确定手性碳原子上所连接的四个基团,并将其排序。
这里我们假设其大小关系为\({a > b > c > d}\) > 2. 我们将\({d}\)放在后面,使得前三个基团\({a, b, c}\)面向自己 > 3. 按照从大到小的循序,即\({a \to b \to c}\)来进行轮转 > 4. 如果轮转的方向是顺时针,那么是\({R}\)构型,如果是逆时针,那么是\({S}\)构型 > > 补充: > 如何判断基团大小? > 1. 基团的大小取决于与手性碳相连的原子的原子序数大小,原子序数越大,基团大小越大。 > 2. 如果与手性谈相连的原子相同,则根据该原子相邻的原子的原子序数确定基团大小。命名举例如下:
- Fischer投影式:
> Fischer投影式 > > + 规定横键的两个基团朝前,竖键的两个基团朝后 > + 碳链直立,编号小的碳原子放在上面(标准的Fischer投影式) > + 投影式在纸面上的操作规则: > - 不能离开纸面翻转 > - 在纸面上向左或向右旋转180°,构型保持不变 > - 在纸面上旋转90°或270°后变成它的对映体 > - 任意两个基团对调一次后变成它的对映体 > 如何从一般的命名转化为Fischer投影式?个人推荐的方法是: >名称 —> 键线式 —> 纽曼投影式 —> (锯架式) —> Fischer投影式
> > 后几步的具体演示可见下图,清晰说明了如何从纽曼投影式到Fishcer投影式: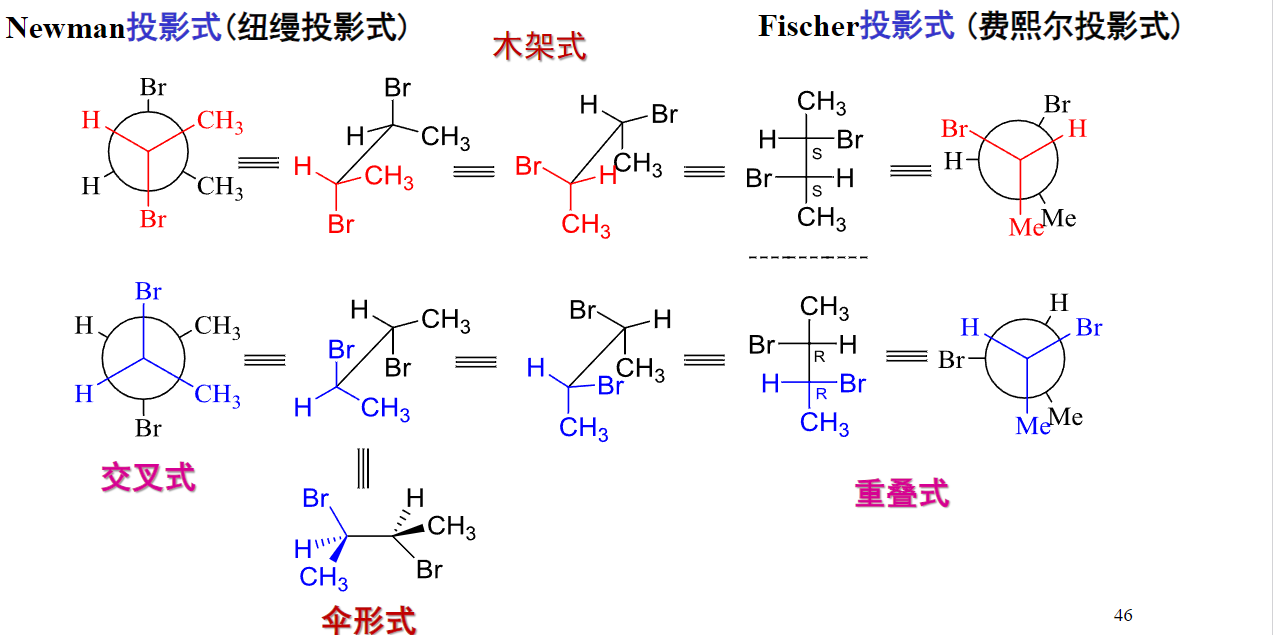
- D/L标记法: > D/L标记法: > + 基于甘油醛作为参照标准物 > + 在Fischer投影式中,甘油醛的羟基(-OH)在右侧为D型,在左侧为L型 > + 在同一类化合物中,与标准物的构型相同为D型,相反为L型 > + 主要用于标记糖类和氨基酸的相对构型 > + D/L构型与旋光性(d/l)无直接关系
3.4 含多个手性碳原子的化合物
3.4.1 立体异构间的关系
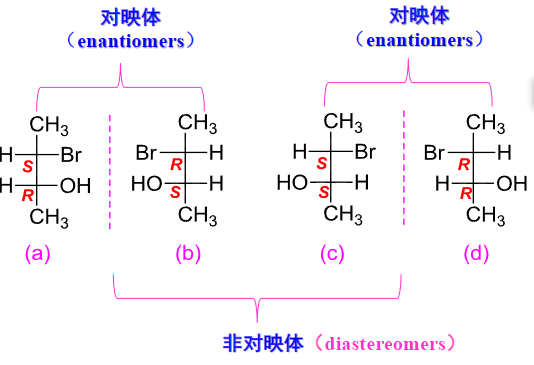
如果一个化合物存在两个手性碳原子,那么它存在四种立体异构体,其中两两成对互为对映异构体。
值得注意的是,不同对对映体之间的关系是非对映的。
3.4.2 更多手性碳与内消旋体
对于含有n个不同的手性碳原子,那么其存在\({2^n}\)个立体异构体。
值得注意的是,之所以要强调不同,是因为倘若有两个完全相同的手性碳原子,但是其手性相反,则构成内消旋体(与外消旋体区分),内消旋体无手性,即使其存在手性碳原子。
值得注意的是,对于内消旋体的命名,通常为在前加上meso-,例如:meso-2, 3-二溴丁烷。
3.5 环状化合物的立体异构
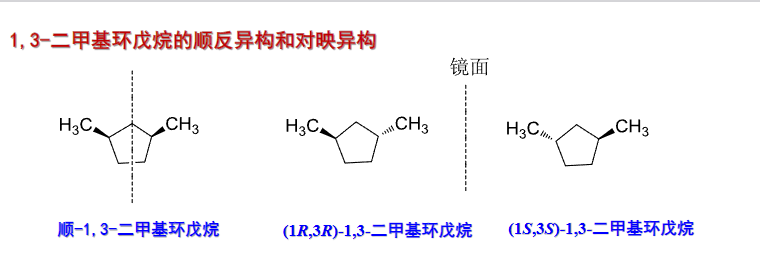
首先要注意的是,在环状化合物中,立体异构和顺反异构通常一起存在,命名的规则是:
这里举例如何判断环的立体异构:
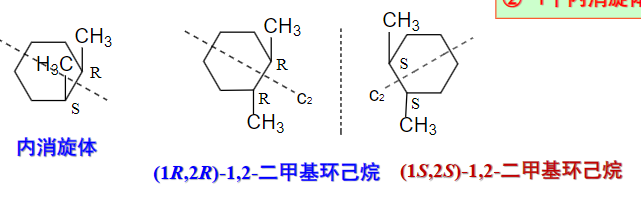
直接从平面结构上来看,简单又方便,与立体结构来判断的结论是一样的!
更多例子:
3.6 不含手性碳原子的化合物
不含手性碳,能不能站着把手性拿下!
有的兄弟,有的,还记得之前说过的丙二烯型化合物可能存在手性吗,其中就存在一条手性轴:
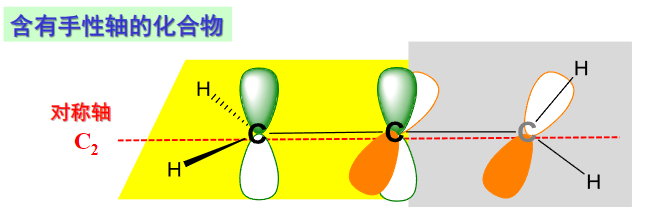
因为右侧的双键的平面与左侧的并不重合,从而产生一条具有手性的轴,比如下面这个:
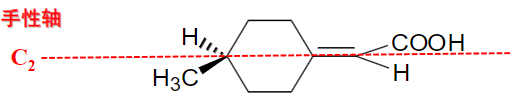
当然,环外双键型化合物也可能存在手性轴:
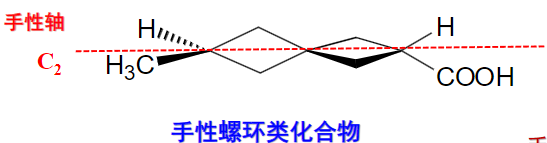
之前说过的螺环也有可能(σ>=<)σ!
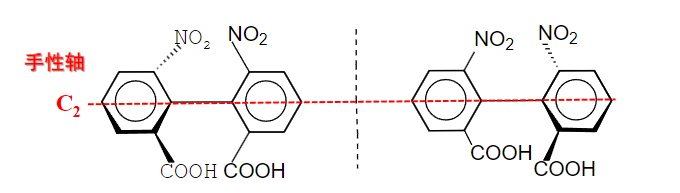
当然还有手性的联苯类:
3.7 手性轴与对映异构
有关手性轴的化合物,目前主要有三类:
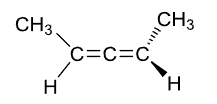
- 丙二烯型化合物的手性轴
- 形如\({\ce{R1R2C=C=CR3R4}}\)
- 当\({\ce{R1\neq R2}}\)且\({\ce{R3\neq R4}}\)时存在手性轴
- 例如\({\ce{CH3CH=C=CHCH3}}\)中,由于两个末端双键平面互相垂直
- 这种情况下不能通过旋转使分子与其镜像重合
- 联苯型化合物的手性轴
- 当\({\ce{C-C}}\)轴两侧各有不同取代基时形成手性
- 由于空间位阻,两个苯环不能自由旋转
- 形成所谓的"旋转受阻"导致手性轴
- 称为轴手性或轴对映异构
- 螺环化合物的手性轴
- 存在一个共同的螺原子连接两个环
- 当两个环不在同一平面且不对称时产生手性
- 螺环两侧的基团排列方式不同
- 不能通过旋转使分子与其镜像重合
值得注意的是,螺环与丙二烯在产生手性轴的原因上是有相似之处的。
3.8 手性化合物的制备
3.8.1 外消旋体的拆分
- 化学拆分法:将原本的对映体做化学反应后得到非对映体,使得其物理性质产生显著不同,便于分离(柱色谱等等)。
- 不对称合成法:利用催化剂使得不同手性化合物的合成倾向不同。
- 酶拆分:自然存在特定手性的酶,会选择特定手性的化合物而反应。